Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dai, Albert
2015.
High-resolution simulations of downslope gravity currents in the acceleration phase.
Physics of Fluids,
Vol. 27,
Issue. 7,
Longo, S.
Ungarish, M.
Di Federico, V.
Chiapponi, L.
and
Addona, F.
2016.
Gravity currents produced by constant and time varying inflow in a circular cross-section channel: Experiments and theory.
Advances in Water Resources,
Vol. 90,
Issue. ,
p.
10.
Dai, Albert
and
Huang, Yu-lin
2016.
High-resolution simulations of non-Boussinesq downslope gravity currents in the acceleration phase.
Physics of Fluids,
Vol. 28,
Issue. 2,
Ottolenghi, L.
Adduce, C.
Inghilesi, R.
Roman, F.
and
Armenio, V.
2016.
Mixing in lock-release gravity currents propagating up a slope.
Physics of Fluids,
Vol. 28,
Issue. 5,
Ottolenghi, L.
Adduce, C.
Roman, F.
and
Armenio, V.
2017.
Analysis of the flow in gravity currents propagating up a slope.
Ocean Modelling,
Vol. 115,
Issue. ,
p.
1.
Dai, Albert
2017.
Experiments on two-layer density-stratified inertial gravity currents.
Physical Review Fluids,
Vol. 2,
Issue. 7,
Ungarish, Marius
2018.
Thin-layer models for gravity currents in channels of general cross-section area, a review .
Environmental Fluid Mechanics,
Vol. 18,
Issue. 1,
p.
283.
Romanic, Djordje
Nicolini, Edoardo
Hangan, Horia
Burlando, Massimiliano
and
Solari, Giovanni
2020.
A novel approach to scaling experimentally produced downburst-like impinging jet outflows.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 196,
Issue. ,
p.
104025.
Dai, Albert
and
Huang, Yu-Lin
2020.
Experiments on gravity currents propagating on unbounded uniform slopes.
Environmental Fluid Mechanics,
Vol. 20,
Issue. 6,
p.
1637.
Wu, Ching-Sen
and
Dai, Albert
2020.
Experiments on two-layer stratified gravity currents in the slumping phase.
Journal of Hydraulic Research,
Vol. 58,
Issue. 5,
p.
831.
Wu, Ching-Sen
and
Ouyang, Huei-Tau
2020.
Flow morphology in bottom-propagating gravity currents over immersed obstacles.
AIP Advances,
Vol. 10,
Issue. 11,
Dai, Albert
and
Huang, Yu-Lin
2021.
Boussinesq and non-Boussinesq gravity currents propagating on unbounded uniform slopes in the deceleration phase.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
De Falco, M.C.
Adduce, C.
Negretti, M.E.
and
Hopfinger, E.J.
2021.
On the dynamics of quasi-steady gravity currents flowing up a slope.
Advances in Water Resources,
Vol. 147,
Issue. ,
p.
103791.
Okon, Samuel Ukpong
Zhong, Qiang
and
He, Zhiguo
2021.
Experimental study on the vertical motion of colliding gravity currents.
Physics of Fluids,
Vol. 33,
Issue. 1,
Canepa, Federico
Burlando, Massimiliano
Romanic, Djordje
Solari, Giovanni
and
Hangan, Horia
2022.
Experimental investigation of the near-surface flow dynamics in downburst-like impinging jets.
Environmental Fluid Mechanics,
Vol. 22,
Issue. 4,
p.
921.
Canepa, Federico
Burlando, Massimiliano
Romanic, Djordje
Solari, Giovanni
and
Hangan, Horia
2022.
Downburst-like experimental impinging jet measurements at the WindEEE Dome.
Scientific Data,
Vol. 9,
Issue. 1,
Wu, Ching-Sen
2024.
Head-on collision of gravity currents of unequal strengths: Large-eddy simulations and laboratory experiments.
Physics of Fluids,
Vol. 36,
Issue. 9,
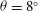 ${\it\theta}=8^{\circ }$ . Unlike gravity currents in a channel, the current head is observed in experiments to be more turbulent when propagating in a V-shaped valley. The turbulence is presumably enhanced due to the lateral flows down the sloping sides of the valley. As a consequence, lateral momentum transport contributes to the observed lower initial speeds. A Wentzel–Kramers–Brillouin like theory predicting the deceleration of the current as it runs upslope agrees remarkably well with simulations and with most experiments, within errors.
${\it\theta}=8^{\circ }$ . Unlike gravity currents in a channel, the current head is observed in experiments to be more turbulent when propagating in a V-shaped valley. The turbulence is presumably enhanced due to the lateral flows down the sloping sides of the valley. As a consequence, lateral momentum transport contributes to the observed lower initial speeds. A Wentzel–Kramers–Brillouin like theory predicting the deceleration of the current as it runs upslope agrees remarkably well with simulations and with most experiments, within errors.

