Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Lei
Li, Jin-Xuan
Liu, Shu-Xue
and
Fan, Yu-Ping
2020.
Experimental and Numerical Studies on the Focused Waves Generated by Double Wave Groups.
Frontiers in Energy Research,
Vol. 8,
Issue. ,
Li, Binbin
2020.
Multi-body hydrodynamic resonance and shielding effect of vessels parallel and nonparallel side-by-side.
Ocean Engineering,
Vol. 218,
Issue. ,
p.
108188.
Tan, Lei
Cheng, Liang
and
Ikoma, Tomoki
2021.
Damping of piston mode resonance between two fixed boxes.
Physics of Fluids,
Vol. 33,
Issue. 6,
Zhao, Wenhua
Taylor, P.H.
and
Wolgamot, H.A.
2021.
Design waves and statistics of linear gap resonances in random seas.
Flow,
Vol. 1,
Issue. ,
Liang, Hui
Chua, Kie Hian
Wang, Hong Chao
and
Choo, Yoo Sang
2021.
Numerical and experimental investigations into fluid resonance in a gap between two side-by-side vessels.
Applied Ocean Research,
Vol. 111,
Issue. ,
p.
102581.
Euvé, Leo-Paul
Pham, Kim
Petitjeans, Philippe
Pagneux, Vincent
and
Maurel, Agnès
2021.
Time domain modelling of a Helmholtz resonator analogue for water waves.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Ren, Xiudi
and
Tao, Longbin
2021.
Nonlinear hydrodynamic characteristics of multi-body platform system.
European Journal of Mechanics - B/Fluids,
Vol. 89,
Issue. ,
p.
509.
Zhao, W.
Taylor, P.H.
Wolgamot, H.A.
and
Eatock Taylor, R.
2021.
Gap resonance from linear to quartic wave excitation and the structure of nonlinear transfer functions.
Journal of Fluid Mechanics,
Vol. 926,
Issue. ,
Zhang, Chongwei
Sun, Xiaotong
Ding, Zhenyu
Chen, Lifen
and
Ning, Dezhi
2021.
Hydrodynamics of a floating barge adjacent to fixed structure in transient wave fronts.
Physics of Fluids,
Vol. 33,
Issue. 10,
Zhang, Hengming
Zhou, Binzhen
Zang, Jun
Vogel, Christopher
Jin, Peng
and
Ning, Dezhi
2021.
Optimization of a three-dimensional hybrid system combining a floating breakwater and a wave energy converter array.
Energy Conversion and Management,
Vol. 247,
Issue. ,
p.
114717.
Zhu, Ling
Zou, Meiyan
Chen, Mingsheng
and
Li, Lin
2021.
Nonlinear dynamic analysis of float-over deck installation for a GBS platform based on a constant parameter time domain model.
Ocean Engineering,
Vol. 235,
Issue. ,
p.
109443.
Liu, Jinshi
Gao, Junliang
Shi, Huabin
Zang, Jun
and
Liu, Qian
2022.
Investigations on the second-order transient gap resonance induced by focused wave groups.
Ocean Engineering,
Vol. 263,
Issue. ,
p.
112430.
Huang, H.C.
Yang, Y.F.
Zhu, R.H.
and
Wang, C.Z.
2022.
Nonlinear wave resonance due to oscillations of twin cylinders in a uniform current.
Applied Ocean Research,
Vol. 121,
Issue. ,
p.
103096.
Zhao, Wenhua
Molin, B.
Wang, Y.
Wolgamot, H.A.
and
Taylor, P.H.
2022.
Nonlinear harmonics of gap fluid resonance with floating body motions.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Zhou, Bin-zhen
Wang, Yu
Zhang, Heng-ming
Jin, Peng
Wang, Lei
and
Zhou, Zhao-min
2022.
Wave Extraction and Attenuation Performance of A Hybrid System of An Edinburgh Duck WEC and A Floating Breakwater.
China Ocean Engineering,
Vol. 36,
Issue. 2,
p.
167.
Shao, Dong
Zheng, Jinhai
Wang, Gang
Fan, Xiang
and
Zhou, Feng
2022.
Influence of bottom slope on gap resonance behavior between fixed body and back wall in close proximity.
Ocean Engineering,
Vol. 265,
Issue. ,
p.
112459.
Zhou, Jiaqi
Ren, Junsheng
and
Bai, Weiwei
2023.
Survey on hydrodynamic analysis of ship–ship interaction during the past decade.
Ocean Engineering,
Vol. 278,
Issue. ,
p.
114361.
Lan, Jun-jie
Jiang, Sheng-chao
and
Gao, Jun-liang
2023.
Hydrodynamic Behavior of Fluid Resonance Between Twin Boxes in Moonpool with Various Edge Profiles Under Wave Actions.
China Ocean Engineering,
Vol. 37,
Issue. 4,
p.
547.
Jing, Penglin
He, Guanghua
Ghassemi, Hassan
and
Luan, Zhengxiao
2023.
Transient responses of the linear and nonlinear gap resonances in the fixed and free-heaving moonpools.
Physics of Fluids,
Vol. 35,
Issue. 8,
Jing, Penglin
He, Guanghua
Chen, Bangqi
Zhang, Cheng
and
Ng, Bingfeng
2023.
Effects of roll motion on linear and nonlinear gap resonances in a moonpool excited by various incident-wave heights.
Physics of Fluids,
Vol. 35,
Issue. 10,
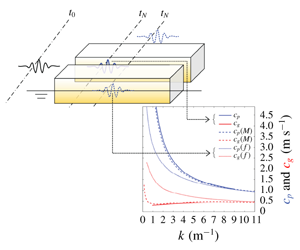
 $m=2$ gap mode is as significant as that of the
$m=2$ gap mode is as significant as that of the  $m=1$ mode. Gap resonance can be driven through different mechanisms, e.g. linear excitation and a nonlinear frequency-doubling process. Significant wave group structure is shown in the gap, and the group structure is more distinct in the case with frequency doubling, i.e. long wave, excitation. Then it is clearer visually that the groups originate at the end of the gap, propagate along the gap and are then partially reflected from the other end. The groups within the gap are very clear because the group velocity is close to constant for the first few gap resonance modes, and much smaller than that for free waves on the open sea. In contrast, the phase speed of waves in the gap is larger than that for free waves outside. Only in the limit of short waves do the group velocity and phase speed of the gap modes tend to those of deep-water free waves. The group and phase speeds from these experiments match well the theoretical forms given by Molin et al. (Appl. Ocean Res., vol. 24 (5), 2002, pp. 247–260), albeit for a slightly different box cross-sectional shape.
$m=1$ mode. Gap resonance can be driven through different mechanisms, e.g. linear excitation and a nonlinear frequency-doubling process. Significant wave group structure is shown in the gap, and the group structure is more distinct in the case with frequency doubling, i.e. long wave, excitation. Then it is clearer visually that the groups originate at the end of the gap, propagate along the gap and are then partially reflected from the other end. The groups within the gap are very clear because the group velocity is close to constant for the first few gap resonance modes, and much smaller than that for free waves on the open sea. In contrast, the phase speed of waves in the gap is larger than that for free waves outside. Only in the limit of short waves do the group velocity and phase speed of the gap modes tend to those of deep-water free waves. The group and phase speeds from these experiments match well the theoretical forms given by Molin et al. (Appl. Ocean Res., vol. 24 (5), 2002, pp. 247–260), albeit for a slightly different box cross-sectional shape.
