Article contents
Insights into the dynamics ofspray–swirl interactions
Published online by Cambridge University Press: 24 November 2016
Abstract
The near-field breakup and interaction of a hollow-cone liquid sheet with coannular swirling air flow have been examined using high-speed diagnostics. Time-resolved PIV (particle image velocimetry; 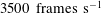 $3500~\text{frames}~\text{s}^{-1}$ ) is employed to capture the spatio-temporal behaviour of the swirling air flow field. The combined liquid–gas phase interaction is visualized with the help of high-speed (
$3500~\text{frames}~\text{s}^{-1}$ ) is employed to capture the spatio-temporal behaviour of the swirling air flow field. The combined liquid–gas phase interaction is visualized with the help of high-speed ( 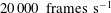 $20\,000~\text{frames}~\text{s}^{-1}$ ) shadowgraphy. In this study, the transition from weak to strong spray–swirl interaction is explained based on the momentum ratio. Proper orthogonal decomposition (POD) is implemented on instantaneous PIV and shadowgraphy images to extract the energetic spatial eigenmodes and characteristic modal frequencies. The POD results suggest the dominance of the KH (Kelvin–Helmholtz) instability mechanism (pure axial shear, axial plus azimuthal shear) in swirl–spray interaction. In addition, linear stability analysis also shows the destabilization of the liquid–air interface caused by KH waves (
$20\,000~\text{frames}~\text{s}^{-1}$ ) shadowgraphy. In this study, the transition from weak to strong spray–swirl interaction is explained based on the momentum ratio. Proper orthogonal decomposition (POD) is implemented on instantaneous PIV and shadowgraphy images to extract the energetic spatial eigenmodes and characteristic modal frequencies. The POD results suggest the dominance of the KH (Kelvin–Helmholtz) instability mechanism (pure axial shear, axial plus azimuthal shear) in swirl–spray interaction. In addition, linear stability analysis also shows the destabilization of the liquid–air interface caused by KH waves ( 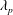 $\unicode[STIX]{x1D706}_{p}$ ), which arises from the formation of a vorticity layer of thickness
$\unicode[STIX]{x1D706}_{p}$ ), which arises from the formation of a vorticity layer of thickness 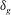 $\unicode[STIX]{x1D6FF}_{g}$ near the liquid–air interface. The frequency values obtained from the primary KH wavelength (
$\unicode[STIX]{x1D6FF}_{g}$ near the liquid–air interface. The frequency values obtained from the primary KH wavelength ( 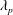 $\unicode[STIX]{x1D706}_{p}$ ) exhibit good agreement with the POD modal frequencies. Scaling laws are proposed to elucidate the relationships between the global length scales (breakup length, spray spread) and the primary wavelength. The breakup length scale and liquid sheet oscillations are meticulously analysed in the time domain to reveal the breakup dynamics of the liquid sheet. Furthermore, the large-scale coherent structures of the swirl flow exhibit different sheet breakup phenomena in the spatial domain. For instance, flapping breakup is induced by the central toroidal recalculation zone in the swirling flow field. Finally, the ligament formation mechanism and its diameter, i.e. the size of first-generation droplets, are measured with phase Doppler interferometry. The measured sizes scale reasonably with KH waves.
$\unicode[STIX]{x1D706}_{p}$ ) exhibit good agreement with the POD modal frequencies. Scaling laws are proposed to elucidate the relationships between the global length scales (breakup length, spray spread) and the primary wavelength. The breakup length scale and liquid sheet oscillations are meticulously analysed in the time domain to reveal the breakup dynamics of the liquid sheet. Furthermore, the large-scale coherent structures of the swirl flow exhibit different sheet breakup phenomena in the spatial domain. For instance, flapping breakup is induced by the central toroidal recalculation zone in the swirling flow field. Finally, the ligament formation mechanism and its diameter, i.e. the size of first-generation droplets, are measured with phase Doppler interferometry. The measured sizes scale reasonably with KH waves.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 61
- Cited by


