Hostname: page-component-66d9dcfd78-9877g Total loading time: 0 Render date: 2026-08-08T06:39:12.117Z Has data issue: false hasContentIssue false
  • English
  • Français

The instability of gyrotactically trapped cell layers

Published online by Cambridge University Press:  15 April 2019

Smitha Maretvadakethope Open the ORCID record for Smitha Maretvadakethope [Opens in a new window] ,
Eric E. Keaveny  and
Yongyun Hwang Open the ORCID record for Yongyun Hwang [Opens in a new window]
Smitha Maretvadakethope
Affiliation:
Department of Mathematics, Imperial College London, South Kensington, London SW7 2AZ, UK
Eric E. Keaveny
Affiliation:
Department of Mathematics, Imperial College London, South Kensington, London SW7 2AZ, UK
Yongyun Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
*
†Email address for correspondence: y.hwang@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Several metres below the coastal ocean surface there are areas of high ecological activity that contain thin layers of concentrated motile phytoplankton. Gyrotactic trapping has been proposed as a potential mechanism for layer formation of bottom-heavy swimming algae cells, especially in flows where the vorticity varies linearly with depth (Durham et al., Science, vol. 323(5917), 2009, pp. 1067–1070). Using a continuum model for dilute microswimmer suspensions, we report that an instability of a gyrotactically trapped cell layer can arise in a pressure-driven plane channel flow. The linear stability analysis reveals that the equilibrium cell-layer solution is hydrodynamically unstable due to negative microswimmer buoyancy (i.e. a gravitational instability) over a range of biologically relevant parameter values. The critical cell concentration for this instability is found to be 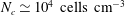$N_{c}\simeq 10^{4}~\text{cells}~\text{cm}^{-3}$, a value comparable to the typical maximum cell concentration observed in thin layers. This result indicates that the instability may be a potential mechanism for limiting the layer’s maximum cell concentration, especially in regions where turbulence is weak, and motivates the study of its nonlinear evolution, perhaps, in the presence of turbulence.

JFM classification

Biological Fluid Dynamics: Bioconvection

Information

Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 868 , 10 June 2019 , R5
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bees, M. & Hill, N. 1997 Wavelengths of bioconvection patterns. J. Expl Biol. 200 (10), 1515–1526.Google Scholar
Bees, M. A. & Hill, N. A. 1998 Linear bioconvection in a suspension of randomly swimming, gyrotactic micro-organisms. Phys. Fluids 10 (8), 1864–1881.10.1063/1.869704Google Scholar
Clifton, W., Bearon, R. N. & Bees, M. A. 2018 Enhanced sedimentation of elongated plankton in simple flows. IMA J. Appl. Maths 83 (4), 743–766.10.1093/imamat/hxy024Google Scholar
Croze, O. A., Ashraf, E. E. & Bees, M. A. 2010 Sheared bioconvection in a horizontal tube. Phys. Biol. 7 (4), 046001.10.1088/1478-3975/7/4/046001Google Scholar
Dekshenieks, M. M., Donaghay, P. L., Sullivan, J. M., Rines, J. E. B., Osborn, T. R. & Twardowski, M. S. 2001 Temporal and spatial occurrence of thin phytoplankton layers in relation to physical processes. Mar. Ecol. Prog. Ser. 223, 61–71.10.3354/meps223061Google Scholar
Durham, W. M., Clement, E., Berry, M., Lillio, F., De Boffetta, G., Cencini, M. & Stocker, R. 2013 Turbulence drives microscale patches of motile phytoplankton. Nat. Comm. 4, 2148.10.1038/ncomms3148Google Scholar
Durham, W. M., Kessler, J. O. & Stocker, R. 2009 Disruption of vertical motility by shear triggers formation of thin phytoplankton layers. Science 323 (5917), 1067–1070.10.1126/science.1167334Google Scholar
Durham, W. M. & Stocker, R. 2012 Thin phytoplankton layers: characteristics, mechanisms, and consequences. Annu. Rev. Marine Sci. 4, 177–207.10.1146/annurev-marine-120710-100957Google Scholar
Franks, P. J. S. 1995 Thin layers of phytoplankton: a model of formation by near-inertial wave shear. Deep-Sea Res. I 42 (1), 75–91.10.1016/0967-0637(94)00028-QGoogle Scholar
Ginzburg, M. & Ginzburg, B. Z. 1985 Influence of age of culture and light intensity on solute concentrations in two Dunaliella strains. J. Exp. Botany 36 (5), 701–712.10.1093/jxb/36.5.701Google Scholar
Grünbaum, D. 2009 Peter principle packs a peck of phytoplankton. Science 323 (5917), 1022–1023.10.1126/science.1170662Google Scholar
Hill, N. A. & Bees, M. A. 2002 Taylor dispersion of gyrotactic swimming micro-organisms in a linear flow. Phys. Fluids 14 (8), 2598–2605.10.1063/1.1458003Google Scholar
Hwang, Y. & Pedley, T. J. 2014a Bioconvection under uniform shear: linear stability analysis. J. Fluid Mech. 738, 522–562.10.1017/jfm.2013.604Google Scholar
Hwang, Y. & Pedley, T. J. 2014b Stability of downflowing gyrotactic microorganism suspensions in a two-dimensional vertical channel. J. Fluid Mech. 749, 750–777.10.1017/jfm.2014.251Google Scholar
Ishikawa, T. & Pedley, T. J. 2007 The rheology of a semi-dilute suspension of swimming model micro-organisms. J. Fluid Mech. 588, 399–435.10.1017/S0022112007007835Google Scholar
Jiménez, F., Rodríguez, J., Bautista, B. & Rodríguez, V. 1987 Relations between chlorophyll, phytoplankton cell abundance and biovolume during a winter bloom in Mediterranean coastal waters. J. Exp. Mar. Bio. Ecol. 105 (2–3), 161–173.10.1016/0022-0981(87)90169-9Google Scholar
Johnston, T. M. S. & Rudnick, D. L. 2009 Observations of the transition layer. J. Phys. Oceanogr. 39 (3), 780–797.10.1175/2008JPO3824.1Google Scholar
Kessler, J. O. 1984 Gyrotactic buoyant convection and spontaneous pattern formation in algal cell cultures. In Nonequilibrium Cooperative Phenomena in Physics and Related Fields, pp. 241–248. Springer.10.1007/978-1-4684-8568-4_14Google Scholar
Kessler, J. O. 1985 Hydrodynamic focusing of motile algal cells. Nature 313 (5999), 218–220.10.1038/313218a0Google Scholar
Krivtsov, V., Bellinger, E. G. & Sigee, D. C. 2000 Changes in the elemental composition of Asterionella formosa during the diatom spring bloom. J. Plankton Res. 22 (1), 169–184.10.1093/plankt/22.1.169Google Scholar
MacIntyre, J. G., Cullen, J. J. & Cembella, A. D. 1997 Vertical migration, nutrition and toxicity in the dinoflagellate Alexandrium tamarense . Mar. Ecol. Prog. Ser. 148, 201–216.10.3354/meps148201Google Scholar
Moline, M. A., Benoit-Bird, K. J., Robbins, I. C., Schroth-Miller, M., Waluk, C. M. & Zelenke, B. 2010 Integrated measurements of acoustical and optical thin layers II: horizontal length scales. Cont. Shelf Res. 30 (1), 29–38.10.1016/j.csr.2009.08.004Google Scholar
Nielsen, T. G., Kiørboe, T. & Bjørnsen, P. K. 1990 Effects of a Chrysochromulina polylepis subsurface bloom on the planktonic community. Mar. Ecol. Prog. Ser. 62, 21–35.Google Scholar
Osborn, T. 1998 Finestructure, microstructure, and thin layers. Oceanography 11, 36–43.Google Scholar
Pedley, T. J. 2010 Instability of uniform micro-organism suspensions revisited. J. Fluid Mech. 647, 335–359.10.1017/S0022112010000108Google Scholar
Pedley, T. J., Hill, N. A. & Kessler, J. O. 1988 The growth of bioconvection patterns in a uniform suspension of gyrotactic micro-organisms. J. Fluid Mech. 195, 223–237.10.1017/S0022112088002393Google Scholar
Pedley, T. J. & Kessler, J. O. 1987 The orientation of spheroidal microorganisms swimming in a flow field. Proc. R. Soc. Lond. B 231 (1262), 47–70.Google Scholar
Pedley, T. J. & Kessler, J. O. 1990 A new continuum model for suspensions of gyrotactic micro-organisms. J. Fluid Mech. 212, 155–182.Google Scholar
Pedley, T. J. & Kessler, J. O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24 (1), 313–358.10.1146/annurev.fl.24.010192.001525Google Scholar
Rusconi, R., Guasto, J. S. & Stocker, R. 2014 Bacterial transport suppressed by fluid shear. Nat. Phys. 10 (3), 212–217.10.1038/nphys2883Google Scholar
Ryan, J. P., McManus, M. A. & Sullivan, J. M. 2010 Interacting physical, chemical and biological forcing of phytoplankton thin-layer variability in Monterey Bay, California. Cont. Shelf Res. 30 (1), 7–16.10.1016/j.csr.2009.10.017Google Scholar
Santamaria, F., De Lillo, F., Cencini, M. & Boffetta, G. 2014 Gyrotactic trapping in laminar and turbulent Kolmogorov flow. Phys. Fluids 26 (11), 111901.10.1063/1.4900956Google Scholar
Similä, A. 1988 Spring development of a chlamydomonas population in Lake Nimetön, a small humic forest lake in southern Finland. In Flagellates in Freshwater Ecosystems, pp. 149–157. Springer.10.1007/978-94-009-3097-1_12Google Scholar
Stacey, M. T., McManus, M. A. & Steinbuck, J. V. 2007 Convergences and divergences and thin layer formation and maintenance. Limnol. Oceanogr. 52 (4), 1523–1532.10.4319/lo.2007.52.4.1523Google Scholar
Steinbuck, J. V., Stacey, M. T., McManus, M. A., Cheriton, O. M. & Ryan, J. P. 2009 Observations of turbulent mixing in a phytoplankton thin layer: implications for formation, maintenance, and breakdown. Limnol. Oceanogr. 54 (4), 1353–1368.10.4319/lo.2009.54.4.1353Google Scholar
Sullivan, J. M., Donaghay, P. L. & Rines, J. E. B. 2010 Coastal thin layer dynamics: consequences to biology and optics. Cont. Shelf Res. 30 (1), 50–65.10.1016/j.csr.2009.07.009Google Scholar