Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-23T06:06:51.964Z Has data issue: false hasContentIssue false
  • English
  • Français

Interactions between two deformable droplets in tandem subjected to impulsive acceleration by surrounding flows

Published online by Cambridge University Press:  30 August 2011

Shaoping Quan ,
Jing Lou  and
Howard A. Stone
Shaoping Quan*
Affiliation:
Institute of High Performance Computing, 1 Fusionopolis Way, No. 16-16 Connexis, Singapore 138632, Singapore
Jing Lou
Affiliation:
Institute of High Performance Computing, 1 Fusionopolis Way, No. 16-16 Connexis, Singapore 138632, Singapore
Howard A. Stone
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: quansp@ihpc.a-star.edu.sg
Get access Rights & Permissions [Opens in a new window]

Abstract

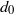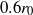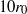The dynamics of two deformable drops placed in tandem and subjected to a sudden acceleration by a gaseous flow is investigated. A finite-volume scheme coupled with the method of moving mesh interface tracking is employed. The unsteady interactions between the droplet pair are studied by varying the minimum initial separation distance () from to with 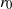being the radius of the initial spherical droplets. The influence of the interactions on the droplet dynamics is examined by comparing with the case of a single isolated droplet at three initial Weber numbers 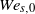of 40, 4 and 0.4. The computations show that for small initial separation distances the dynamics of the downstream droplet is significantly affected by the presence of the upstream droplet. A mushroom shape is formed by the droplet pair at the two largest Weber numbers, while the two drops experience small deformation and shape oscillations at 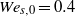. The drag coefficient of the downstream droplet is dramatically reduced, especially for the two largest Weber numbers with smaller initial separation distances due to the sheltering effects, while the drag force of the upstream drop is slightly decreased. For the cases with smaller 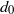, a thin film is formed between the two drops at the later stages, and this leads to a sudden increase in the drag of the trailing drop, but a sharp reduction in the drag of the leading drop.

JFM classification

Drops and Bubbles: Drops Multiphase and Particle-laden Flows: Multiphase flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 684 , 10 October 2011 , pp. 384 - 406
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Aalburg, C., van Leer, B. & Faeth, G. M. 2003 Deformation and drag properties of round drops subjected to shock-wave disturbances. AIAA J. 41, 2371–2378.CrossRefGoogle Scholar
2. Chang, W., Giraldo, F. & Perot, B. 2002 Analysis of an exact fractional step method. J. Comput. Phys. 180, 183–199.CrossRefGoogle Scholar
3. Chi, B. K. & Leal, L. G. 1989 A theoretical study of the motion of a viscous drop toward a fluid interface at low Reynolds number. J. Fluid Mech. 201, 123–146.CrossRefGoogle Scholar
4. Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops, and Particles. Academic.Google Scholar
5. Dai, M. Z. & Schmidt, D. P. 2005a Adaptive tetrahedral meshing in free-surface flow. J. Comput. Phys. 208, 228–252.CrossRefGoogle Scholar
6. Dai, M. Z. & Schmidt, D. P. 2005b Numerical simulation of head-on droplet collision: effect of viscosity on maximum deformation. Phys. Fluids 17, 041701.CrossRefGoogle Scholar
7. Esmaeeli, A. & Tryggvason, G. 1998 Direct numerical simulations of bubbly flows. Part 1. Low Reynolds number arrays. J. Fluid Mech. 377, 313–345.CrossRefGoogle Scholar
8. Esmaeeli, A. & Tryggvason, G. 1999 Direct numerical simulations of bubbly flows. Part 2. Moderate Reynolds number arrays. J. Fluid Mech. 385, 325–358.CrossRefGoogle Scholar
9. Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a newtonian fluid. Part 1. Sedimentation. J. Fluid Mech. 261, 95–134.CrossRefGoogle Scholar
10. Harper, J. F. 1970 On bubbles rising in line at large Reynolds numbers. J. Fluid Mech. 41, 751–758.CrossRefGoogle Scholar
11. Hsiang, L. P. & Faeth, G. M. 1992 Near-limit drop deformation and secondary breakup. Intl J. Multiphase Flow 18, 635–652.CrossRefGoogle Scholar
12. Hsiang, L. P. & Faeth, G. M. 1995 Drop deformation and breakup due to shock wave and steady disturbances. Intl J. Multiphase Flow 21, 545–560.CrossRefGoogle Scholar
13. Joseph, D. D., Belanger, J. & Beavers, G. S. 1999 Breakup of a liquid drop suddenly exposed to a high-speed airstream. Intl J. Multiphase Flow 25, 1263–1303.CrossRefGoogle Scholar
14. Kim, I., Elghobashi, S. & Sirignano, W. A. 1993 Three-dimensional flow over two spheres placed side by side. J. Fluid Mech. 246, 465–488.CrossRefGoogle Scholar
15. Kim, S., Hwang, J. W. & Lee, C. S. 2010 Experiments and modeling on droplet motion and atomization of diesel and bio-diesel fuels in a cross-flowed air stream. Intl J. Heat Fluid Flow 31, 667–679.CrossRefGoogle Scholar
16. Kumari, N. & Abraham, J. 2008 Interactions of decelerating drops moving in tandem. Atomiz. Sprays 18, 191–241.CrossRefGoogle Scholar
17. Lamb, H 1945 Hydrodynamics. Dover Publications.Google Scholar
18. Lee, C. H. & Reitz, R. D. 2000 An experimental study of the effect of gas density on the distortion and breakup mechanism of drops in high speed gas stream. Intl J. Multiphase Flow 26, 229–244.CrossRefGoogle Scholar
19. Legendre, D., Magnaudet, J. & Mougin, G. 2003 Hydrodynamic interactions between two spherical bubbles rising side by side in a viscous liquid. J. Fluid Mech. 497, 133–166.CrossRefGoogle Scholar
20. Liu, D. Y., Anders, K. & Frohn, A. 1988 Drag coefficients of single droplets moving in an infinite droplet chain on the axis of a tube. Intl J. Multiphase Flow 14, 217–232.CrossRefGoogle Scholar
21. Liu, X. D., Fedkiw, R. P. & Kang, M. J. 2000 A boundary condition capturing method for Poisson’s equation on irregular domains. J. Comput. Phys. 160, 151–178.CrossRefGoogle Scholar
22. Magnaudet, J & Eames, I 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.CrossRefGoogle Scholar
23. Manga, M. & Stone, H. A. 1993 Buoyancy-driven interactions between two deformable viscous drops. J. Fluid Mech. 256, 647–683.CrossRefGoogle Scholar
24. Manga, M. & Stone, H. A. 1995 Low Reynolds number motion of bubbles, drops and rigid spheres through fluid–fluid interfaces. J. Fluid Mech. 287, 279–298.CrossRefGoogle Scholar
25. Mashayek, A. & Ashgriz, N. 2009 Model for deformation of drops and liquid jets in gaseous crossflows. AIAA J. 47, 303–313.CrossRefGoogle Scholar
26. Mulholland, J. A., Srivastava, R. K. & Wendt, J. O. L. 1988 Influence of droplet spacing on drag coefficient in nonevaporating, monodisperse streams. AIAA J. 26, 1231–1237.CrossRefGoogle Scholar
27. Nguyen, Q. V. & Dunn-Rankin, D. 1992 Experiments examining drag in linear droplet packets. Exp. Fluids 12, 157–165.CrossRefGoogle Scholar
28. Perot, B. 2000 Conservation properties of unstructured staggered mesh schemes. J. Comput. Phys. 159, 58–89.CrossRefGoogle Scholar
29. Perot, B. & Nallapati, R. 2003 A moving unstructured staggered mesh method for the simulation of incompressible free-surface flows. J. Comput. Phys. 184, 192–214.CrossRefGoogle Scholar
30. Poo, J. Y. & Ashgriz, N. 1991 Variation of drag coefficients in an interacting drop stream. Exp. Fluids 11, 1–8.CrossRefGoogle Scholar
31. Quan, S. P. 2011 Simulations of multiphase flows with multiple length scales using moving mesh interface tracking with adaptive meshing. J. Comput. Phys. 230, 5430–5448.CrossRefGoogle Scholar
32. Quan, S. P., Lou, J. & Schmidt, D. P. 2009a Modeling merging and breakup in the moving mesh interface tracking method for multiphase flow simulations. J. Comput. Phys. 228, 2660–2675.CrossRefGoogle Scholar
33. Quan, S. P. & Schmidt, D. P. 2006 Direct numerical study of a liquid droplet impulsively accelerated by gaseous flow. Phys. Fluids 18, 102103.CrossRefGoogle Scholar
34. Quan, S. P. & Schmidt, D. P. 2007 A moving mesh interface tracking method for 3d incompressible two-phase flows. J. Comput. Phys. 221, 761–780.CrossRefGoogle Scholar
35. Quan, S. P., Schmidt, D. P., Hua, J. S. & Lou, J. 2009b A numerical study of the relaxation and breakup of an elongated drop in a viscous liquid. J. Fluid Mech. 640, 235–264.CrossRefGoogle Scholar
36. Raju, M. S. & Sirignano, W. A. 1990 Interaction between two vaporizing droplets in an intermediate Reynolds number flow. Phys. Fluids A 2, 1780–1796.CrossRefGoogle Scholar
37. Sangani, A. S. & Didwania, A. K. 1993 Dynamics simulations of flows of bubbly liquids at large Reynolds numbers. J. Fluid Mech. 250, 307–437.CrossRefGoogle Scholar
38. Simpkins, P. G. & Bales, E. L. 1972 Water-drop response to sudden accelerations. J. Fluid Mech. 55, 629–639.CrossRefGoogle Scholar
39. Smereka, P. 1993 On the motion of bubbles in a periodic box. J. Fluid Mech. 254, 79–112.CrossRefGoogle Scholar
40. Temkin, S. & Ecker, G. Z. 1989 Droplet pair interactions in a shock-wave flow field. J. Fluid Mech. 202, 467–497.CrossRefGoogle Scholar
41. Temkin, S. & Kim, S. S. 1980 Droplet motion induced by weak shock waves. J. Fluid Mech. 96, 133–157.CrossRefGoogle Scholar
42. Temkin, S. & Mehta, M. K. 1982 Droplet drag in an accelerating and decelerating flow. J. Fluid Mech. 116, 297–313.CrossRefGoogle Scholar
43. Tsamopoulos, J., Dimakopoulos, Y., Chatzidai, N., Karapetsas, G. & Pavlidis, M. 2008 Steady bubble rise and deformation in Newtonian and viscoplastic fluids and conditions for bubble entrapment. J. Fluid Mech. 601, 123–164.CrossRefGoogle Scholar
44. Wadhwa, A. R., Magi, V. & Abraham, J. 2007 Transient deformation and drag of decelerating drops in axisymmetric flows. Phys. Fluids 19, 113301.CrossRefGoogle Scholar
45. Warnica, W. D., Renksizbulut, M. & Strong, A. B. 1995a Drag coefficients of spherical liquid droplets Part 1: quiescent gaseous fields. Exp. Fluids 18, 258–264.CrossRefGoogle Scholar
46. Warnica, W. D., Renksizbulut, M. & Strong, A. B. 1995b Drag coefficients of spherical liquid droplets Part 2: turbulent gaseous fields. Exp. Fluids 18, 265–275.CrossRefGoogle Scholar
47. van Wijngaarden, L. 2005 Bubble velocities induced by trailing vortices behind neighbours. J. Fluid Mech. 541, 203–229.CrossRefGoogle Scholar
48. Xu, Q. & Basaran, O. A. 2007 Computational analysis of drop-on-demand drop formation. Phys. Fluids 19, 102111.CrossRefGoogle Scholar
49. Yiantsios, S. G. & Davis, R. H. 1990 On the buoyancy-driven motion of a drop towards a rigid surface or a deformable interface. J. Fluid Mech. 217, 547–573.CrossRefGoogle Scholar
50. Yuan, H. & Prosperetti, A. 1994 On the in-line motion of two spherical bubbles in a viscous fluid. J. Fluid Mech. 278, 325–349.CrossRefGoogle Scholar
51. Zhang, X., Schmidt, D. & Perot, B. 2002 Accuracy and conservation properties of a three-dimensional unstructured staggered mesh scheme for fluid dynamics. J. Comput. Phys. 175, 764–791.CrossRefGoogle Scholar
52. Zinchenko, A. Z., Rother, M. A & Davis, R. H. 1997 A novel boundary-integral algorithm for viscous interaction of deformable drops. Phys. Fluids 9 (6), 1493–1511.CrossRefGoogle Scholar
53. Zinchenko, A. Z., Rother, M. A. & Davis, R. H. 1999 Cusping, capture, and breakup of interacting drops by a curvatureless boundary-integral algorithm. J. Fluid Mech. 391, 249–292.CrossRefGoogle Scholar