Hostname: page-component-758b78586c-wkjwp Total loading time: 0 Render date: 2023-11-29T19:22:16.840Z Has data issue: false Feature Flags: { "corePageComponentGetUserInfoFromSharedSession": true, "coreDisableEcommerce": false, "useRatesEcommerce": true } hasContentIssue false
  • English
  • Français

The Jeffery–Hamel similarity solution and its relation to flow in a diverging channel

Published online by Cambridge University Press:  07 November 2011

P. E. Haines ,
R. E. Hewitt  and
A. L. Hazel
P. E. Haines*
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL, UK
R. E. Hewitt
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL, UK
A. L. Hazel
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL, UK
*
†Email address for correspondence: philip.haines@adelaide.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

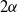We explore the relevance of the idealized Jeffery–Hamel similarity solution to the practical problem of flow in a diverging channel of finite (but large) streamwise extent. Numerical results are presented for the two-dimensional flow in a wedge of separation angle , bounded by circular arcs at the inlet/outlet and for a net radial outflow of fluid. In particular, we show that in a finite domain there is a sequence of nested neutral curves in the 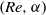plane, each corresponding to a midplane symmetry-breaking (pitchfork) bifurcation, where 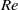is a Reynolds number based on the radial mass flux. For small wedge angles we demonstrate that the first pitchfork bifurcation in the finite domain occurs at a critical Reynolds number that is in agreement with the only pitchfork bifurcation in the infinite-domain similarity solution, but that the criticality of the bifurcation differs (in general). We explain this apparent contradiction by demonstrating that, for 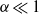, superposition of two (infinite-domain) eigenmodes can be used to construct a leading-order finite-domain eigenmode. These constructed modes accurately predict the multiple symmetry-breaking bifurcations of the finite-domain flow without recourse to computation of the full field equations. Our computational results also indicate that temporally stable, isolated, steady solutions may exist. These states are finite-domain analogues of the steady waves recently presented by Kerswell, Tutty, & Drazin (J. Fluid Mech., vol. 501, 2004, pp. 231–250) for an infinite domain. Moreover, we demonstrate that there is non-uniqueness of stable solutions in certain parameter regimes. Our numerical results tie together, in a consistent framework, the disparate results in the existing literature.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Mathematical Foundations: General fluid mechanics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 687 , 25 November 2011 , pp. 404 - 430
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: School of Mathematical Sciences, University of Adelaide, Adelaide, SA 5005, Australia.

References

1. Akulenko, L. D. & Kumakshev, S. A. 2008 Bifurcation of multimode flows of a viscous fluid in a plane diverging channel. J. Appl. Math. Mech. 72 (3), 296–302.Google Scholar
2. Banks, W. H. H., Drazin, P. G. & Zaturska, M. B. 1988 On perturbations of Jeffery–Hamel flow. J. Fluid Mech. 186, 559–581.Google Scholar
3. Cliffe, K. A. & Greenfield, A. C. 1982 Some comments on laminar flow in symmetric two dimensional channels. Harwell Report AERE-TP 939.Google Scholar
4. Cliffe, K. A., Spence, A. & Tavener, S. J. 2000 The numerical analysis of bifurcation problems with application to fluid mechanics. Acta Numerica 9, 39–131.Google Scholar
5. Dean, W. R. 1934 Note on the divergent flow of fluid. Phil. Mag. 18 (7), 759–777.Google Scholar
6. Dennis, S. C. R., Banks, W. H. H., Drazin, P. G. & Zaturska, M. B. 1997 Flow along a diverging channel. J. Fluid Mech. 336, 183–202.Google Scholar
7. Drazin, P. G. 1995 Stability of flow in a diverging channel. In Stability and Wave Propagation in Fluids and Solids (ed. Galdi, G. P. ). pp. 39–65. Springer.Google Scholar
8. Fearn, R. M., Mullin, T. & Cliffe, K. A. 1990 Nonlinear flow phenomena in a symmetric sudden expansion. J. Fluid Mech. 211, 595–608.Google Scholar
9. Fraenkel, L. E. 1962 Laminar flow in symmetrical channels with slightly curved walls. I. On the Jeffery–Hamel Solutions for flow between plane walls. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 267 (1328), 119–138.Google Scholar
10. Goldshtik, M., Hussain, F. & Shtern, V. 1991 Symmetry breaking in vortex-source and Jeffery–Hamel flows. J. Fluid Mech. 232, 521–566.Google Scholar
11. Gresho, P. M. & Sani, R. L. 1998 Incompressible Flow and the Finite Element Method: Volume 1, Advection–Diffusion and Isothermal Laminar Flow. John Wiley & Sons.Google Scholar
12. Haines, P. E. 2010 The Jeffery–Hamel similarity solution and its relation to flow in a diverging channel. PhD thesis, The University of Manchester.Google Scholar
13. Hamadiche, M., Scott, J. & Jeandel, D. 1994 Temporal stability of Jeffery–Hamel flow. J. Fluid Mech. 268, 71–88.Google Scholar
14. Hamel, G. 1916 Spiralförmige Bewegungen zäher Flüssigkeiten. Jahresbericht der Deutschen Mathematiker Vereinigung 25, 34–60.Google Scholar
15. Heil, M. & Hazel, A. L. 2006 oomph-lib– An object-oriented multi-physics finite-element library. In Fluid-Structure Interaction (ed. Schafer, M. & Bungartz, H.-J. ). Lecture Notes in Computational Science and Engineering 53. pp. 19–49. Springer.Google Scholar
16. Hewitt, R. E. & Hazel, A. L. 2007 Midplane-symmetry breaking in the flow between two counter-rotating disks. J. Engng Maths 57 (3), 273–288.Google Scholar
17. Jeffery, G. B. 1915 The two-dimensional steady motion of a viscous fluid. Phil. Mag. 6 (29), 455–465.Google Scholar
18. Kerswell, R. R., Tutty, O. R. & Drazin, P. G. 2004 Steady nonlinear waves in diverging channel flow. J. Fluid Mech. 501, 231–250.Google Scholar
19. Kuznetsov, Y. A. 1998 Elements of Applied Bifurcation Theory. Springer.Google Scholar
20. Putkaradze, V. & Vorobieff, P. 2006 Instabilities, bifurcations, and multiple solutions in expanding channel flows. Phys. Rev. Lett. 97 (14), 144502.Google Scholar
21. Rosenhead, L. 1940 The steady two-dimensional radial flow of viscous fluid between two inclined plane walls. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. (1934–1990) 175 (963), 436–467.Google Scholar
22. Salinger, A. G., Bou-Rabee, N. M., Pawlowski, R. P., Wilkes, E. D., Burroughs, E. A., Lehoucq, R. B. & Romero, L. A. 2002 LOCA 1.0 Library of continuation algorithms: theory and implementation manual. Tech. Rep. SAND2002-0396. Sandia National Laboratories.Google Scholar
23. Sobey, I. J. & Drazin, P. G. 1986 Bifurcations of two-dimensional channel flows. J. Fluid Mech. 171, 263–287.Google Scholar
24. Sobey, I. J. & Mullin, T. 1993 Calculation of multiple solutions for the two-dimensional Navier–Stokes equations. Numer. Meth. Fluid Dyn. 4, 417.Google Scholar
25. Tutty, O. R. 1996 Nonlinear development of flow in channels with non-parallel walls. J. Fluid Mech. 326, 265–284.Google Scholar
26. Yu, Z., Shao, X. & Lin, J. 2010 Numerical computations of the flow in a finite diverging channel. J. Zhejiang Univ.-Science A 11 (1), 50–60.Google Scholar
27. Zienkiewicz, O. C. & Zhu, J. Z. 1992 The superconvergent patch recovery and a posteriori error estimates. Part 1: the recovery technique. Intl J. Numer. Meth. Engng 33 (7), 1331–1364.Google Scholar