Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bury, Yannick
and
Jardin, Thierry
2012.
Transitions to chaos in the wake of an axisymmetric bluff body.
Physics Letters A,
Vol. 376,
Issue. 45,
p.
3219.
Feng, Li-Hao
and
Wang, Jin-Jun
2013.
Particle image velocimetry study of parameter influence for synthetic-jet application.
Flow Measurement and Instrumentation,
Vol. 34,
Issue. ,
p.
53.
Bury, Yannick
and
Jardin, Thierry
2014.
Turbulence and Interactions.
Vol. 125,
Issue. ,
p.
31.
Jardin, T.
and
David, L.
2014.
Spanwise gradients in flow speed help stabilize leading-edge vortices on revolving wings.
Physical Review E,
Vol. 90,
Issue. 1,
Jardin, Thierry
and
Bury, Yannick
2014.
Distributed forcing of the flow past a blunt-based axisymmetric bluff body.
Theoretical and Computational Fluid Dynamics,
Vol. 28,
Issue. 3,
p.
259.
Feng, Li-Hao
and
Wang, Jin-Jun
2014.
Modification of a circular cylinder wake with synthetic jet: Vortex shedding modes and mechanism.
European Journal of Mechanics - B/Fluids,
Vol. 43,
Issue. ,
p.
14.
Shaafi, K.
and
Vengadesan, S.
2014.
Wall proximity effects on the effectiveness of upstream control rod.
Journal of Fluids and Structures,
Vol. 49,
Issue. ,
p.
112.
Liu, Ya-Guang
and
Feng, Li-Hao
2015.
Suppression of lift fluctuations on a circular cylinder by inducing the symmetric vortex shedding mode.
Journal of Fluids and Structures,
Vol. 54,
Issue. ,
p.
743.
Dawson, Scott T.
Schiavone, Nicole K.
Rowley, Clarence W.
and
Williams, David R.
2015.
A Data-Driven Modeling Framework for Predicting Forces and Pressures on a Rapidly Pitching Airfoil.
Jardin, T.
and
David, L.
2015.
Coriolis effects enhance lift on revolving wings.
Physical Review E,
Vol. 91,
Issue. 3,
Wang, Chenglei
Tang, Hui
Duan, Fei
and
Yu, Simon C.M.
2016.
Control of wakes and vortex-induced vibrations of a single circular cylinder using synthetic jets.
Journal of Fluids and Structures,
Vol. 60,
Issue. ,
p.
160.
Dawson, Scott T. M.
Hemati, Maziar S.
Williams, Matthew O.
and
Rowley, Clarence W.
2016.
Characterizing and correcting for the effect of sensor noise in the dynamic mode decomposition.
Experiments in Fluids,
Vol. 57,
Issue. 3,
Shaafi, K.
Naik, Sandeep N.
and
Vengadesan, S.
2017.
Effect of rotating cylinder on the wake-wall interactions.
Ocean Engineering,
Vol. 139,
Issue. ,
p.
275.
Rowley, Clarence W.
and
Dawson, Scott T.M.
2017.
Model Reduction for Flow Analysis and Control.
Annual Review of Fluid Mechanics,
Vol. 49,
Issue. 1,
p.
387.
Wang, Chenglei
Tang, Hui
Yu, Simon C. M.
and
Duan, Fei
2017.
Lock-on of vortex shedding to a pair of synthetic jets with phase difference.
Physical Review Fluids,
Vol. 2,
Issue. 10,
Ma, Li-Qun
and
Feng, Li-Hao
2019.
Vortex formation and evolution for flow over a circular cylinder excited by symmetric synthetic jets.
Experimental Thermal and Fluid Science,
Vol. 104,
Issue. ,
p.
89.
Hazel, S
Huang, Y
and
amirat, M Ait
2019.
Numerical Investigation of a New Single Vortex Generation Technique.
IOP Conference Series: Materials Science and Engineering,
Vol. 616,
Issue. 1,
p.
012026.
Hazel, Soufyane
Huang, Yong
and
Ait Amirat, Mokhtar
2021.
New single vortex generation method for flame/vortex interaction using flow behind a rotating cylinder.
Fluid Dynamics Research,
Vol. 53,
Issue. 6,
p.
065506.
Sun, Lei
Huang, Yong
Wang, Xiwei
Feng, Xiang
and
Xiao, Wei
2021.
High Frequency Characteristics of the Near Wake and Vortex Past a Triangular Cylinder.
Journal of Fluids Engineering,
Vol. 143,
Issue. 3,
Ping, Huan
Zhu, Hongbo
Zhang, Kai
Zhou, Dai
Bao, Yan
Xu, Yuwang
and
Han, Zhaolong
2021.
Dynamic mode decomposition based analysis of flow past a transversely oscillating cylinder.
Physics of Fluids,
Vol. 33,
Issue. 3,
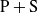 can be observed, depending on the forcing frequency and the momentum coefficient, highlighting remarkable analogies with oscillating cylinders.
can be observed, depending on the forcing frequency and the momentum coefficient, highlighting remarkable analogies with oscillating cylinders.
