Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vinuesa, Ricardo
Örlü, Ramis
Sanmiguel Vila, Carlos
Ianiro, Andrea
Discetti, Stefano
and
Schlatter, Philipp
2017.
Revisiting History Effects in Adverse-Pressure-Gradient Turbulent Boundary Layers.
Flow, Turbulence and Combustion,
Vol. 99,
Issue. 3-4,
p.
565.
Bobke, A.
Vinuesa, R.
Örlü, R.
and
Schlatter, P.
2017.
History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
667.
Dróżdż, A.
and
Elsner, W.
2017.
An experimental study of turbulent boundary layers approaching separation.
International Journal of Heat and Fluid Flow,
Vol. 68,
Issue. ,
p.
337.
Vinuesa, R.
Negi, P.S.
Atzori, M.
Hanifi, A.
Henningson, D.S.
and
Schlatter, P.
2018.
Turbulent boundary layers around wing sections up to Rec=1,000,000.
International Journal of Heat and Fluid Flow,
Vol. 72,
Issue. ,
p.
86.
Lee, Young Mo
Jung, Wongwan
Lee, Jae Hwa
and
Kim, Jooha
2018.
Direct numerical simulations of temporally decelerating turbulent pipe flows.
Journal of Mechanical Science and Technology,
Vol. 32,
Issue. 8,
p.
3713.
Simens, M.P.
and
Gungor, A.G.
2018.
Influence of the transition of a laminar separation bubble on the downstream evolution of strong adverse pressure gradient turbulent boundary layers.
European Journal of Mechanics - B/Fluids,
Vol. 67,
Issue. ,
p.
70.
Yoon, Min
Hwang, Jinyul
and
Sung, Hyung Jin
2018.
Contribution of large-scale motions to the skin friction in a moderate adverse pressure gradient turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
p.
288.
Niegodajew, Paweł
Dróżdż, Artur
and
Elsner, Witold
2019.
A new approach for estimation of the skin friction in turbulent boundary layer under the adverse pressure gradient conditions.
International Journal of Heat and Fluid Flow,
Vol. 79,
Issue. ,
p.
108456.
Vaquero, J.
Renard, N.
and
Deck, S.
2019.
Advanced simulations of turbulent boundary layers under pressure-gradient conditions.
Physics of Fluids,
Vol. 31,
Issue. 11,
Lee, Jae Hwa
Sung, Hyung Jin
and
Adrian, Ronald J.
2019.
Space–time formation of very-large-scale motions in turbulent pipe flow.
Journal of Fluid Mechanics,
Vol. 881,
Issue. ,
p.
1010.
Vaquero, J.
Renard, N.
and
Deck, S.
2019.
Effects of upstream perturbations on the solution of the laminar and fully turbulent boundary layer equations with pressure gradients.
Physics of Fluids,
Vol. 31,
Issue. 12,
Dharmarathne, Suranga
Bocanegra Evans, Humberto
Hamed, Ali M.
Aksak, Burak
Chamorro, Leonardo P.
Tutkun, Murat
Doosttalab, Ali
and
Castillo, Luciano
2019.
On the large- and small-scale motions in a separated, turbulent-boundary-layer flow.
Journal of Turbulence,
Vol. 20,
Issue. 9,
p.
563.
Wenzel, Christoph
Gibis, Tobias
Kloker, Markus
and
Rist, Ulrich
2019.
Self-similar compressible turbulent boundary layers with pressure gradients. Part 1. Direct numerical simulation and assessment of Morkovin’s hypothesis.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
239.
Wang, Xu
Wang, Zhenguo
Sun, Mingbo
Wang, Qiancheng
and
Hu, Zhiwei
2019.
Direct numerical simulation of a supersonic turbulent boundary layer subject to adverse pressure gradient induced by external successive compression waves.
AIP Advances,
Vol. 9,
Issue. 8,
p.
085215.
Sanmiguel Vila, C.
Vinuesa, R.
Discetti, S.
Ianiro, A.
Schlatter, P.
and
Örlü, R.
2020.
Separating adverse-pressure-gradient and Reynolds-number effects in turbulent boundary layers.
Physical Review Fluids,
Vol. 5,
Issue. 6,
Fan, Yitong
Li, Weipeng
Atzori, Marco
Pozuelo, Ramon
Schlatter, Philipp
and
Vinuesa, Ricardo
2020.
Decomposition of the mean friction drag in adverse-pressure-gradient turbulent boundary layers.
Physical Review Fluids,
Vol. 5,
Issue. 11,
Yang, Jongmin
Yoon, Min
and
Sung, Hyung Jin
2020.
The turbulent/non-turbulent interface in an adverse pressure gradient turbulent boundary layer.
International Journal of Heat and Fluid Flow,
Vol. 86,
Issue. ,
p.
108704.
Sakai, Takahiro
Diamessis, Peter J.
and
Jacobs, Gustaaf B.
2020.
Self-sustained instability, transition, and turbulence induced by a long separation bubble in the footprint of an internal solitary wave. II. Flow statistics.
Physical Review Fluids,
Vol. 5,
Issue. 10,
Tanarro, Álvaro
Mallor, Fermín
Offermans, Nicolas
Peplinski, Adam
Vinuesa, Ricardo
and
Schlatter, Philipp
2020.
Enabling Adaptive Mesh Refinement for Spectral-Element Simulations of Turbulence Around Wing Sections.
Flow, Turbulence and Combustion,
Vol. 105,
Issue. 2,
p.
415.
Tanarro, Á.
Vinuesa, R.
and
Schlatter, P.
2020.
Effect of adverse pressure gradients on turbulent wing boundary layers.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
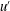 $u^{\prime }$) are frequently observed in the log region of a zero pressure gradient turbulent boundary layer, and that these motions significantly influence near-wall small-scale
$u^{\prime }$) are frequently observed in the log region of a zero pressure gradient turbulent boundary layer, and that these motions significantly influence near-wall small-scale 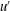 $u^{\prime }$-structures by modulating the amplitude (Hutchins & Marusic, J. Fluid Mech., vol. 579, 2007, pp. 1–28; Mathis et al., J. Fluid Mech., vol. 628, 2009, pp. 311–337). In the present study, we provide evidence that the spatial organization of large-scale structures in the log region is significantly influenced by the strength of adverse pressure gradients in turbulent boundary layers based on a direct numerical simulation dataset. For a mild adverse pressure gradient boundary layer flow, groups of hairpin vortices are coherently aligned in the streamwise direction to form hairpin vortex packets, and streamwise merging events of the induced large-scale
$u^{\prime }$-structures by modulating the amplitude (Hutchins & Marusic, J. Fluid Mech., vol. 579, 2007, pp. 1–28; Mathis et al., J. Fluid Mech., vol. 628, 2009, pp. 311–337). In the present study, we provide evidence that the spatial organization of large-scale structures in the log region is significantly influenced by the strength of adverse pressure gradients in turbulent boundary layers based on a direct numerical simulation dataset. For a mild adverse pressure gradient boundary layer flow, groups of hairpin vortices are coherently aligned in the streamwise direction to form hairpin vortex packets, and streamwise merging events of the induced large-scale 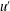 $u^{\prime }$-structures create a larger streamwise length scale of structures than that for a zero pressure gradient boundary layer flow. As the pressure gradient strength increases further, however, the formation of hairpin packets is continuously suppressed, and large-scale motions are consequently not concatenated to create a longer motion, resulting in a significant reduction of the streamwise coherence of large-scale structures in the log layer. Although energy spectrum maps for
$u^{\prime }$-structures create a larger streamwise length scale of structures than that for a zero pressure gradient boundary layer flow. As the pressure gradient strength increases further, however, the formation of hairpin packets is continuously suppressed, and large-scale motions are consequently not concatenated to create a longer motion, resulting in a significant reduction of the streamwise coherence of large-scale structures in the log layer. Although energy spectrum maps for 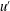 $u^{\prime }$-structures show that the large-scale energy is continuously intensified above the log layer with an increase in the pressure gradient, amplitude modulation of the near-wall small-scale motions is dominantly induced by log region large-scale structures for adverse pressure gradient flows. Conditional averaged flow fields with large-scale Q2 and Q4 events indicate that large-scale counter-rotating roll modes play an important role in organizing the flows under the pressure gradients, and the large-scale roll modes associated with Q4 events are more enhanced in the outer layer than those associated with Q2 events, reducing the streamwise coherence of the vortices in a packet.
$u^{\prime }$-structures show that the large-scale energy is continuously intensified above the log layer with an increase in the pressure gradient, amplitude modulation of the near-wall small-scale motions is dominantly induced by log region large-scale structures for adverse pressure gradient flows. Conditional averaged flow fields with large-scale Q2 and Q4 events indicate that large-scale counter-rotating roll modes play an important role in organizing the flows under the pressure gradients, and the large-scale roll modes associated with Q4 events are more enhanced in the outer layer than those associated with Q2 events, reducing the streamwise coherence of the vortices in a packet.