Article contents
Large-to-small scale frequency modulation analysis in wall-bounded turbulence via visibility networks
Published online by Cambridge University Press: 07 May 2021
Abstract
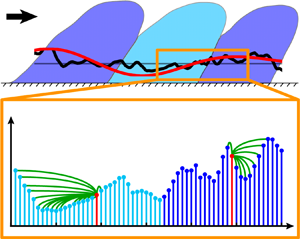
Scale interaction is studied in wall-bounded turbulence by focusing on the frequency modulation (FM) mechanism of the large scales on small-scale velocity fluctuations. Different from the analysis of amplitude modulation (AM), FM has been less investigated owing to the difficulty of developing robust tools for broadband signals. To tackle this issue, the natural visibility graph approach is proposed in this work to map the full velocity signals into complex networks. We show that the network degree centrality is able to capture the signal structure at local scales directly from the full signal, thereby quantifying FM. Velocity signals from numerically-simulated turbulent channel flows and an experimental turbulent boundary layer are investigated at different Reynolds numbers. A correction of Taylor's hypothesis for time series is proposed to overcome the overprediction of near-wall FM obtained when local mean velocity is used as the convective velocity. Results provide network-based evidence of the large-to-small FM features for all the three velocity components in the near-wall region, with a reversal mechanism emerging far from the wall. Additionally, scaling arguments, in view of the quasi-steady quasi-homogeneous hypothesis, are discussed, and a delay time between the large and small scales is detected that is very close to the characteristic time of the near-wall cycle. Results show that the visibility graph is a parameter-free tool that turns out to be effective and robust to detect FM in different configurations of wall-bounded turbulent flows. Based on the present findings, the visibility network-based approach can represent a reliable tool to systematically investigate scale interaction mechanisms in wall-bounded turbulence.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 25
- Cited by


