Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shi, Nan
Emran, Mohammad S.
and
Schumacher, Jörg
2012.
Boundary layer structure in turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 706,
Issue. ,
p.
5.
Chillà, F.
and
Schumacher, J.
2012.
New perspectives in turbulent Rayleigh-Bénard convection.
The European Physical Journal E,
Vol. 35,
Issue. 7,
Bosbach, Johannes
Weiss, Stephan
and
Ahlers, Guenter
2012.
Plume Fragmentation by Bulk Interactions in Turbulent Rayleigh-Bénard Convection.
Physical Review Letters,
Vol. 108,
Issue. 5,
Ślęzak, Andrzej
Grzegorczyn, Sławomir
and
Batko, Kornelia M.
2012.
Resistance Coefficients of Polymer Membrane with Concentration Polarization.
Transport in Porous Media,
Vol. 95,
Issue. 1,
p.
151.
Schmeling, Daniel
Bosbach, Johannes
and
Wagner, Claus
2013.
Oscillations of the large-scale circulation in turbulent mixed convection in a closed rectangular cavity.
Experiments in Fluids,
Vol. 54,
Issue. 5,
Schmeling, Daniel
Bosbach, Johannes
and
Wagner, Claus
2014.
Simultaneous measurement of temperature and velocity fields in convective air flows.
Measurement Science and Technology,
Vol. 25,
Issue. 3,
p.
035302.
Gunasegarane, G. S.
and
Puthenveettil, Baburaj A.
2014.
Dynamics of line plumes on horizontal surfaces in turbulent convection.
Journal of Fluid Mechanics,
Vol. 749,
Issue. ,
p.
37.
Gastine, Thomas
Wicht, Johannes
and
Aurnou, Jonathan M.
2015.
Turbulent Rayleigh–Bénard convection in spherical shells.
Journal of Fluid Mechanics,
Vol. 778,
Issue. ,
p.
721.
Schmeling, Daniel
Bosbach, Johannes
and
Wagner, Claus
2015.
Measurements of the dynamics of thermal plumes in turbulent mixed convection based on combined PIT and PIV.
Experiments in Fluids,
Vol. 56,
Issue. 6,
Nipin, L.
and
Tomar, Gaurav
2015.
Effect of viscosity contrast on plume formation in density stratified fluids.
Chemical Engineering Science,
Vol. 134,
Issue. ,
p.
510.
Ślęzak-Prochazka, Izabella
Batko, Kornelia M.
Wąsik, Sławomir
and
Ślęzak, Andrzej
2016.
$$H^{*}$$ H ∗ Peusner’s Form of the Kedem–Katchalsky Equations for Non-homogenous Non-electrolyte Binary Solutions.
Transport in Porous Media,
Vol. 111,
Issue. 2,
p.
457.
Koothur, Vipin
and
Puthenveettil, Baburaj A.
2016.
Progress in Wall Turbulence 2.
Vol. 23,
Issue. ,
p.
181.
Cardoso, Silvana S.S.
Cartwright, Julyan H.E.
Checa, Antonio G.
and
Sainz-Díaz, C. Ignacio
2016.
Fluid-flow-templated self-assembly of calcium carbonate tubes in the laboratory and in biomineralization: The tubules of the watering-pot shells, Clavagelloidea.
Acta Biomaterialia,
Vol. 43,
Issue. ,
p.
338.
Barge, Laura M.
Cardoso, Silvana S. S.
Cartwright, Julyan H. E.
Doloboff, Ivria J.
Flores, Erika
Macías-Sánchez, Elena
Sainz-Díaz, C. Ignacio
and
Sobrón, Pablo
2016.
Self-assembling iron oxyhydroxide/oxide tubular structures: laboratory-grown and field examples from Rio Tinto.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 472,
Issue. 2195,
p.
20160466.
Sabet, Nasser
Hassanzadeh, Hassan
and
Abedi, Jalal
2017.
Selection of efficient solvent in solvent-aided thermal recovery of bitumen.
Chemical Engineering Science,
Vol. 161,
Issue. ,
p.
198.
Dong, Peixin
Li, Xiaoxiao
Guan, Zhiqiang
and
Gurgenci, Hal
2018.
The transient start-up process of natural draft dry cooling towers in dispatchable thermal power plants.
International Journal of Heat and Mass Transfer,
Vol. 123,
Issue. ,
p.
201.
Praphul, T.
Joshy, P. J.
and
Tide, P. S.
2019.
Numerical Analysis of Plume Structures of Fluids on a Horizontal Heated Plate.
Journal of Heat Transfer,
Vol. 141,
Issue. 4,
Chowdhuri, Subharthi
McNaughton, Keith G.
and
Prabha, Thara V.
2019.
An Empirical Scaling Analysis of Heat and Momentum Cospectra Above the Surface Friction Layer in a Convective Boundary Layer.
Boundary-Layer Meteorology,
Vol. 170,
Issue. 2,
p.
257.
Shevkar, Prafulla P.
Gunasegarane, G. S.
Mohanan, Sanal K.
and
Puthenveettil, Baburaj A.
2019.
Effect of shear on coherent structures in turbulent convection.
Physical Review Fluids,
Vol. 4,
Issue. 4,
Ramareddy, G. V.
Joshy, P. J.
Nair, Gayathri
and
Puthenveettil, Baburaj A.
2020.
Scaling in concentration-driven convection boundary layers with transpiration.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
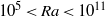 ) and at three Prandtl numbers (
) and at three Prandtl numbers (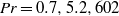 ). Using geometric constraints on the relations for the mean plume spacings, we obtain expressions for the total length of near-wall plumes on horizontal surfaces in turbulent convection. The plume length per unit area (
). Using geometric constraints on the relations for the mean plume spacings, we obtain expressions for the total length of near-wall plumes on horizontal surfaces in turbulent convection. The plume length per unit area (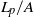 ), made dimensionless by the near-wall length scale in turbulent convection (
), made dimensionless by the near-wall length scale in turbulent convection (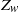 ), remains constant for a given fluid. The Nusselt number is shown to be directly proportional to
), remains constant for a given fluid. The Nusselt number is shown to be directly proportional to  for a given fluid layer of height
for a given fluid layer of height 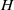 . The increase in
. The increase in 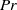 has a weak influence in decreasing
has a weak influence in decreasing 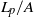 . These expressions match the measurements, thereby showing that the assumption of laminar natural convection boundary layers in turbulent convection is consistent with the observed total length of line plumes. We then show that similar relationships are obtained based on the assumption that the line plumes are the outcome of the instability of laminar natural convection boundary layers on the horizontal surfaces.
. These expressions match the measurements, thereby showing that the assumption of laminar natural convection boundary layers in turbulent convection is consistent with the observed total length of line plumes. We then show that similar relationships are obtained based on the assumption that the line plumes are the outcome of the instability of laminar natural convection boundary layers on the horizontal surfaces.