Article contents
Linear and nonlinear optimal growth mechanisms for generating turbulent bands
Published online by Cambridge University Press: 17 March 2022
Abstract
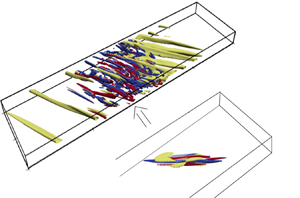
Recently, many authors have investigated the origin and growth of turbulent bands in shear flows, highlighting the role of streaks and their inflectional instability in the process of band generation and sustainment. Recalling that streaks are created by an optimal transient growth mechanism, and motivated by the observation of a strong increase of the disturbance kinetic energy corresponding to the creation of turbulent bands, we use linear and nonlinear energy optimisations in a tilted domain to unveil the main mechanisms allowing the creation of a turbulent band in a channel flow. Linear transient growth analysis shows an optimal growth for wavenumbers having an angle of approximately  $35^\circ$, close to the peak values of the premultiplied energy spectra of direct numerical simulations. This linear optimal perturbation generates oblique streaks, which, for a sufficiently large initial energy, induce turbulence in the whole domain, due to the lack of spatial localisation. However, spatially localised perturbations obtained by adding nonlinear effects to the optimisation or by artificially confining the linear optimal to a localised region in the transverse direction are characterised by a large-scale flow and lead to the generation of a localised turbulent band. These results suggest that two main elements are needed for inducing turbulent bands in a tilted domain: (i) a linear energy growth mechanism, such as the lift-up, for generating large-amplitude flow structures, which produce inflection points; (ii) spatial localisation, linked to the presence or generation of large-scale vortices. We show that these elements alone generate isolated turbulent bands also in large non-tilted domains.
$35^\circ$, close to the peak values of the premultiplied energy spectra of direct numerical simulations. This linear optimal perturbation generates oblique streaks, which, for a sufficiently large initial energy, induce turbulence in the whole domain, due to the lack of spatial localisation. However, spatially localised perturbations obtained by adding nonlinear effects to the optimisation or by artificially confining the linear optimal to a localised region in the transverse direction are characterised by a large-scale flow and lead to the generation of a localised turbulent band. These results suggest that two main elements are needed for inducing turbulent bands in a tilted domain: (i) a linear energy growth mechanism, such as the lift-up, for generating large-amplitude flow structures, which produce inflection points; (ii) spatial localisation, linked to the presence or generation of large-scale vortices. We show that these elements alone generate isolated turbulent bands also in large non-tilted domains.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 6
- Cited by


