Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kaufman, Joshua J.
Tao, Guangming
Shabahang, Soroush
Banaei, Esmaeil-Hooman
Deng, Daosheng S.
Liang, Xiangdong
Johnson, Steven G.
Fink, Yoel
and
Abouraddy, Ayman F.
2012.
Structured spheres generated by an in-fibre fluid instability.
Nature,
Vol. 487,
Issue. 7408,
p.
463.
Kaufman, Joshua J.
Ottman, Richard
Tao, Guangming
Shabahang, Soroush
Banaei, Esmaeil-Hooman
Liang, Xiangdong
Johnson, Steven G.
Fink, Yoel
Chakrabarti, Ratna
and
Abouraddy, Ayman F.
2013.
In-fiber production of polymeric particles for biosensing and encapsulation.
Proceedings of the National Academy of Sciences,
Vol. 110,
Issue. 39,
p.
15549.
Gumennik, Alexander
Wei, Lei
Lestoquoy, Guillaume
Stolyarov, Alexander M.
Jia, Xiaoting
Rekemeyer, Paul H.
Smith, Matthew J.
Liang, Xiangdong
Grena, Benjamin J.-B.
Johnson, Steven G.
Gradečak, Silvija
Abouraddy, Ayman F.
Joannopoulos, John D.
and
Fink, Yoel
2013.
Silicon-in-silica spheres via axial thermal gradient in-fibre capillary instabilities.
Nature Communications,
Vol. 4,
Issue. 1,
Khudiyev, Tural
Tobail, Osama
and
Bayindir, Mehmet
2014.
Tailoring self-organized nanostructured morphologies in kilometer-long polymer fiber.
Scientific Reports,
Vol. 4,
Issue. 1,
Beilharz, D.
Guyon, A.
Li, E. Q.
Thoraval, M.-J.
and
Thoroddsen, S. T.
2015.
Antibubbles and fine cylindrical sheets of air.
Journal of Fluid Mechanics,
Vol. 779,
Issue. ,
p.
87.
Liu, Dan-dan
Xu, Yu-mei
Ding, Xian-ting
Yang, Jian
and
Ma, Zhi-jun
2015.
Utilizing the Plateau-Rayleigh Instability with Heat-Driven Nano-Biosensing Systems.
SLAS Technology,
Vol. 20,
Issue. 4,
p.
463.
Tao, Guangming
Kaufman, Joshua J.
Shabahang, Soroush
Rezvani Naraghi, Roxana
Sukhov, Sergey V.
Joannopoulos, John D.
Fink, Yoel
Dogariu, Aristide
and
Abouraddy, Ayman F.
2016.
Digital design of multimaterial photonic particles.
Proceedings of the National Academy of Sciences,
Vol. 113,
Issue. 25,
p.
6839.
Lü Ming
Ning Zhi
and
Yan Kai
2016.
Comparative study on the spatial evolution of liquid jet under linear and nonlinear stability theories.
Acta Physica Sinica,
Vol. 65,
Issue. 16,
p.
166801.
Xue, Shicheng
Barton, Geoffrey W.
Fleming, Simon
and
Argyros, Alexander
2017.
Analysis of Capillary Instability in Metamaterials Fabrication Using Fiber Drawing Technology.
Journal of Lightwave Technology,
Vol. 35,
Issue. 11,
p.
2167.
Liu, Shuang Xi
and
Lü, Ming
2019.
Nonlinear Evolution and Breakup of the Cavitating Liquid Jet Surrounded by the Rotary Compressible Air.
ACS Omega,
Vol. 4,
Issue. 26,
p.
21732.
Faccini de Lima, Camila
van der Elst, Louis A.
Koraganji, Veda Narayana
Zheng, Mengxin
Gokce Kurtoglu, Merve
and
Gumennik, Alexander
2019.
Towards Digital Manufacturing of Smart Multimaterial Fibers.
Nanoscale Research Letters,
Vol. 14,
Issue. 1,
Lü, Ming
Ning, Zhi
and
Yan, Kai
2019.
Study on the breakup of liquid jet in a coaxial swirling compressible gas flow.
Nonlinear Dynamics,
Vol. 97,
Issue. 2,
p.
1263.
Xu, Bingrui
and
Deng, Daosheng
2020.
Linear analysis of dewetting instability in multilayer planar sheets for composite nanostructures.
Physical Review Fluids,
Vol. 5,
Issue. 8,
Vadivukkarasan, M.
2020.
Transition from absolute to convective instability in a compound jet.
European Journal of Mechanics - B/Fluids,
Vol. 84,
Issue. ,
p.
186.
Farsoiya, Palas Kumar
Roy, Anubhab
and
Dasgupta, Ratul
2020.
Azimuthal capillary waves on a hollow filament – the discrete and the continuous spectrum.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Zhou, Ying
Xi, Shuting
Huang, Yajiang
Kong, Miqiu
Yang, Qi
and
Li, Guangxian
2020.
Preparation of near-spherical PA12 particles for selective laser sintering via Plateau-Rayleigh instability of molten fibers.
Materials & Design,
Vol. 190,
Issue. ,
p.
108578.
Zhang, Jing
Wang, Zhe
and
Wang, Zhixun
2020.
Advanced Fiber Sensing Technologies.
Vol. 9,
Issue. ,
p.
199.
Yan, Wei
Dong, Chaoqun
Xiang, Yuanzhuo
Jiang, Shan
Leber, Andreas
Loke, Gabriel
Xu, Wenxin
Hou, Chong
Zhou, Shifeng
Chen, Min
Hu, Run
Shum, Perry Ping
Wei, Lei
Jia, Xiaoting
Sorin, Fabien
Tao, Xiaoming
and
Tao, Guangming
2020.
Thermally drawn advanced functional fibers: New frontier of flexible electronics.
Materials Today,
Vol. 35,
Issue. ,
p.
168.
Xu, Bingrui
Ma, Shuqi
Xiang, Yuanzhuo
Zhang, Jing
Zhu, Meifang
Wei, Lei
Tao, Guangming
and
Deng, Daosheng
2020.
In-Fiber Structured Particles and Filament Arrays from the Perspective of Fluid Instabilities.
Advanced Fiber Materials,
Vol. 2,
Issue. 1,
p.
1.
Shukla, I.
Wang, F.
Mowlavi, S.
Guyomard, A.
Liang, X.
Johnson, S. G.
and
Nave, J.-C.
2021.
Reduced model for capillary breakup with thermal gradients: Predictions and computational validation.
Physics of Fluids,
Vol. 33,
Issue. 12,
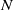 fluids with arbitrary viscosities, thicknesses, densities, and surface tensions in both the Stokes regime and for the full Navier–Stokes problem. Generalizing previous work by Tomotika (
fluids with arbitrary viscosities, thicknesses, densities, and surface tensions in both the Stokes regime and for the full Navier–Stokes problem. Generalizing previous work by Tomotika (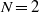 ), Stone & Brenner (
), Stone & Brenner (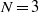 , equal viscosities) and others, we present a full linear stability analysis of the growth modes and rates, reducing the system to a linear generalized eigenproblem in the Stokes case. Furthermore, we demonstrate by Plateau-style geometrical arguments that only axisymmetric instabilities need be considered. We show that the
, equal viscosities) and others, we present a full linear stability analysis of the growth modes and rates, reducing the system to a linear generalized eigenproblem in the Stokes case. Furthermore, we demonstrate by Plateau-style geometrical arguments that only axisymmetric instabilities need be considered. We show that the 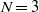 case is already sufficient to obtain several interesting phenomena: limiting cases of thin shells or low shell viscosity that reduce to
case is already sufficient to obtain several interesting phenomena: limiting cases of thin shells or low shell viscosity that reduce to 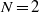 problems, and a system with competing breakup processes at very different length scales. The latter is demonstrated with full three-dimensional Stokes-flow simulations. Many
problems, and a system with competing breakup processes at very different length scales. The latter is demonstrated with full three-dimensional Stokes-flow simulations. Many 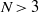 cases remain to be explored, and as a first step we discuss two illustrative
cases remain to be explored, and as a first step we discuss two illustrative 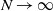 cases, an alternating-layer structure and a geometry with a continuously varying viscosity.
cases, an alternating-layer structure and a geometry with a continuously varying viscosity.
