Article contents
Linear stability of compressible flow in a streamwise corner
Published online by Cambridge University Press: 04 November 2011
Abstract
The linear stability of the compressible flow in a streamwise corner is studied. The steady laminar mean flow is obtained as a solution to the parabolized Navier–Stokes equations with the asymptotic cross-flow velocity enforced on the far-field boundaries via a sponge region and was found to be in good agreement with the corresponding self-similar solution. The eigenvalue problem of linear stability theory is solved for base flows at three different Mach numbers representing the incompressible limit (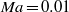 ), the subsonic (
), the subsonic (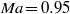 ) and the supersonic (
) and the supersonic (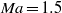 ) velocity regime. Particular attention is given to the subject of wave obliqueness. Owing to the break of periodicity by the opposing wall the exact spanwise wavenumbers and associated phase angles resolved in the computational domain are not known a priori. We address this problem by imposing different phase angles on the far-field boundaries to obtain the critical values of the Reynolds number, streamwise wavenumber and spanwise wavenumber from a three-dimensional solution space. The stability characteristics of the different types of modes present in the spectrum are discussed. An inviscid corner mode with odd-symmetry not present in the subsonic regime and with a higher amplification rate than its symmetric counterpart is identified in the supersonic case. Acoustic modes are found in an enlarged computational domain and categorized with respect to speed, symmetry and wall-boundedness, among them an acoustic corner mode.
) velocity regime. Particular attention is given to the subject of wave obliqueness. Owing to the break of periodicity by the opposing wall the exact spanwise wavenumbers and associated phase angles resolved in the computational domain are not known a priori. We address this problem by imposing different phase angles on the far-field boundaries to obtain the critical values of the Reynolds number, streamwise wavenumber and spanwise wavenumber from a three-dimensional solution space. The stability characteristics of the different types of modes present in the spectrum are discussed. An inviscid corner mode with odd-symmetry not present in the subsonic regime and with a higher amplification rate than its symmetric counterpart is identified in the supersonic case. Acoustic modes are found in an enlarged computational domain and categorized with respect to speed, symmetry and wall-boundedness, among them an acoustic corner mode.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 27
- Cited by

