Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hamlington, Peter E.
Poludnenko, Alexei Y.
and
Oran, Elaine S.
2012.
Intermittency in premixed turbulent reacting flows.
Physics of Fluids,
Vol. 24,
Issue. 7,
Morshed, Khandakar Niaz
Venayagamoorthy, Subhas Karan
and
Dasi, Lakshmi Prasad
2013.
Intermittency and local dissipation scales under strong mean shear.
Physics of Fluids,
Vol. 25,
Issue. 1,
Scheel, Janet D
Emran, Mohammad S
and
Schumacher, Jörg
2013.
Resolving the fine-scale structure in turbulent Rayleigh–Bénard convection.
New Journal of Physics,
Vol. 15,
Issue. 11,
p.
113063.
Yakhot, Victor
2014.
Reynolds number of transition and self-organized criticality of strong turbulence.
Physical Review E,
Vol. 90,
Issue. 4,
Tsinober, Arkady
2014.
The Essence of Turbulence as a Physical Phenomenon.
p.
3.
Vreman, A. W.
and
Kuerten, J. G. M.
2014.
Statistics of spatial derivatives of velocity and pressure in turbulent channel flow.
Physics of Fluids,
Vol. 26,
Issue. 8,
Schumacher, Jörg
Scheel, Janet D.
Krasnov, Dmitry
Donzis, Diego A.
Yakhot, Victor
and
Sreenivasan, Katepalli R.
2014.
Small-scale universality in fluid turbulence.
Proceedings of the National Academy of Sciences,
Vol. 111,
Issue. 30,
p.
10961.
Scheel, Janet D.
and
Schumacher, Jörg
2014.
Local boundary layer scales in turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 758,
Issue. ,
p.
344.
Qiu, Xiang
Liu, Yu-Lu
and
Zhou, Quan
2014.
Local dissipation scales in two-dimensional Rayleigh-Taylor turbulence.
Physical Review E,
Vol. 90,
Issue. 4,
Yakhot, V.
Bartlett, C.
Chen, H.
Shock, R.
Staroselsky, I.
and
Wanderer, J.
2015.
Progress in Hybrid RANS-LES Modelling.
Vol. 130,
Issue. ,
p.
37.
Marchioli, Cristian
and
Soldati, Alfredo
2015.
Turbulent breakage of ductile aggregates.
Physical Review E,
Vol. 91,
Issue. 5,
Bailey, S. C. C.
and
Witte, B. M.
2016.
On the universality of local dissipation scales in turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 786,
Issue. ,
p.
234.
Thompson, Roney L.
Sampaio, Luiz Eduardo B.
de Bragança Alves, Felipe A.V.
Thais, Laurent
and
Mompean, Gilmar
2016.
A methodology to evaluate statistical errors in DNS data of plane channel flows.
Computers & Fluids,
Vol. 130,
Issue. ,
p.
1.
Vreman, A.W.
and
Kuerten, J.G.M.
2016.
A third-order multistep time discretization for a Chebyshev tau spectral method.
Journal of Computational Physics,
Vol. 304,
Issue. ,
p.
162.
Yakhot, Victor
and
Donzis, Diego
2017.
Emergence of Multiscaling in a Random-Force Stirred Fluid.
Physical Review Letters,
Vol. 119,
Issue. 4,
Wei, Yikun
Dou, Hua-Shu
Zhu, Zuchao
Wang, Zhengdao
Qian, Yuehong
and
Xue, Haihong
2017.
Temporal Evolution and Scaling of Mixing in Turbulent Thermal Convection for Inhomogeneous Boundary Conditions.
Advances in Applied Mathematics and Mechanics,
Vol. 9,
Issue. 5,
p.
1035.
Alhamdi, Sabah F. H.
and
Bailey, Sean C. C.
2017.
Universality of local dissipation scales in turbulent boundary layer flows with and without free-stream turbulence.
Physics of Fluids,
Vol. 29,
Issue. 11,
Alhamdi, Sabah F. H.
and
Bailey, Sean C. C.
2018.
External intermittency compensation of dissipation scale distributions in a turbulent boundary layer.
Physical Review Fluids,
Vol. 3,
Issue. 7,
Ganapathisubramani, B.
2018.
Law of the wall for small-scale streamwise turbulence intensity in high-Reynolds-number turbulent boundary layers.
Physical Review Fluids,
Vol. 3,
Issue. 10,
Luo, Jian-ping
Wang, Yong-bo
Qiu, Xiang
Xia, Yu-xian
and
Liu, Yu-lu
2018.
Energy dissipation statistics along the Lagrangian trajectories in three-dimensional turbulent flows.
Journal of Hydrodynamics,
Vol. 30,
Issue. 1,
p.
169.
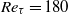 ,
, 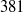 and
and 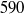 . For sufficiently large
. For sufficiently large 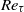 , the dissipation-scale distributions and energy dissipation moments in the channel bulk flow agree with those in homogeneous isotropic turbulence, including only a weak Reynolds-number dependence of both the finest and largest scales. Systematic, but
, the dissipation-scale distributions and energy dissipation moments in the channel bulk flow agree with those in homogeneous isotropic turbulence, including only a weak Reynolds-number dependence of both the finest and largest scales. Systematic, but 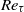 -independent, variations in the distributions and moments arise as the wall is approached for
-independent, variations in the distributions and moments arise as the wall is approached for 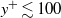 . In the range
. In the range 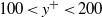 , there are substantial differences in the moments between the lowest and the two larger values of
, there are substantial differences in the moments between the lowest and the two larger values of 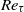 . This is most likely caused by coherent vortices from the near-wall region, which fill the whole channel for low
. This is most likely caused by coherent vortices from the near-wall region, which fill the whole channel for low 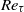 .
.