Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-31T13:20:44.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flows

Published online by Cambridge University Press:  06 June 2013

H. M. Blackburn ,
P. Hall  and
S. J. Sherwin
H. M. Blackburn*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
P. Hall
Affiliation:
Department of Mathematics, Imperial College London, South Kensington, London SW7 2AZ, UK
S. J. Sherwin
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
*
†Email address for correspondence: Hugh.Blackburn@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the development of nonlinear three-dimensional vortex–wave interaction equilibria of laminar plane Couette flow for a range of spanwise wavenumbers. The results are computed using a hybrid approach that captures the required asymptotic structure while at the same time providing a direct link with full numerical calculations of equilibrium states. Each equilibrium state consists of a streak flow, a roll flow and a wave propagating on the streak. Direct numerical simulations at finite Reynolds numbers using initial conditions constructed from these parts confirm that the scheme generates equilibrium solutions of the Navier–Stokes equations. Consideration of the form of the vortex–wave interaction equations in the high-spanwise-wavenumber limit predicts that for small wavelengths the equilibria take on a self-similar structure confined near the centre of the flow. These states feel no influence from the walls, and lead to a class of canonical states relevant to arbitrary shear flows. These predictions are supported by an analysis of computational results at increasing values of the spanwise wavenumber. For the wave part of these new canonical states, it is shown that the mass-specific kinetic energy density per unit wavenumber scales with the 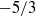$- 5/ 3$ power of the wavenumber.

JFM classification

Boundary Layers: Boundary layer stability Waves/Free-surface Flows: Critical layers Instability: Transition to turbulence

Information

Type
Rapids
Information
Journal of Fluid Mechanics , Volume 726 , 10 July 2013 , R2
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91 (22), 224502.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
Hall, P. & Horseman, N. J. 1991 The linear inviscid secondary instability of longitudinal vortex structures in boundary layers. J. Fluid Mech. 232, 357–375.Google Scholar
Hall, P. & Sherwin, S. J. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. T. 1988 The nonlinear interaction of Tollmein–Schlichting waves and Taylor–Görtler vortices in curved channel flows. Proc. R. Soc. Lond. A 417, 255–282.Google Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Kolmogorov, A. N. 1941 Local structure of turbulence in incompessible viscous fluid at very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Schneider, T. M. & Eckhardt, B 2009 Edge states intermediate between laminar and turbulent states in pipe flow. Phil. Trans. R. Soc. Lond. A 367, 577–587.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–890.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Wang, J., Gibson, J. F. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98 (20), 204501.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar

Blackburn Supplementary Material

Animation of plane Couette flow DNS corresponding to the self-sustaining state shown in figure 4 (black line for k=1). Time runs from t=0 to t=1000. The grey translucent isosurface is drawn at (streamwise velocity component) u=0 and represents the critical layer. Red and blue isosurfaces are equal magnitude positive and negative values of spanwise velocity component (w), and serves to illustrate wave structure.

Download Blackburn Supplementary Material(Video)
Video 3.6 MB