Hostname: page-component-5b777bbd6c-6lqsf Total loading time: 0 Render date: 2025-06-19T20:36:59.728Z Has data issue: false hasContentIssue false
  • English
  • Français

Method of aerodynamic noise source identification for cylinder flows

Published online by Cambridge University Press:  04 June 2025

Yu-Han Zhao Open the ORCID record for Yu-Han Zhao [Opens in a new window] ,
Jue Ding ,
Pei-Fen Weng ,
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window] ,
Yu-Hong Dong Open the ORCID record for Yu-Hong Dong [Opens in a new window]  and
Xiao-Quan Yang Open the ORCID record for Xiao-Quan Yang [Opens in a new window]
Yu-Han Zhao
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, PR China
Jue Ding
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, PR China
Pei-Fen Weng
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, PR China Shanghai University of Electric Power, Shanghai, PR China
Quan Zhou
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, PR China
Yu-Hong Dong
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, PR China
Xiao-Quan Yang*
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, PR China
*
Corresponding author: Xiao-Quan Yang, quanshui@shu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

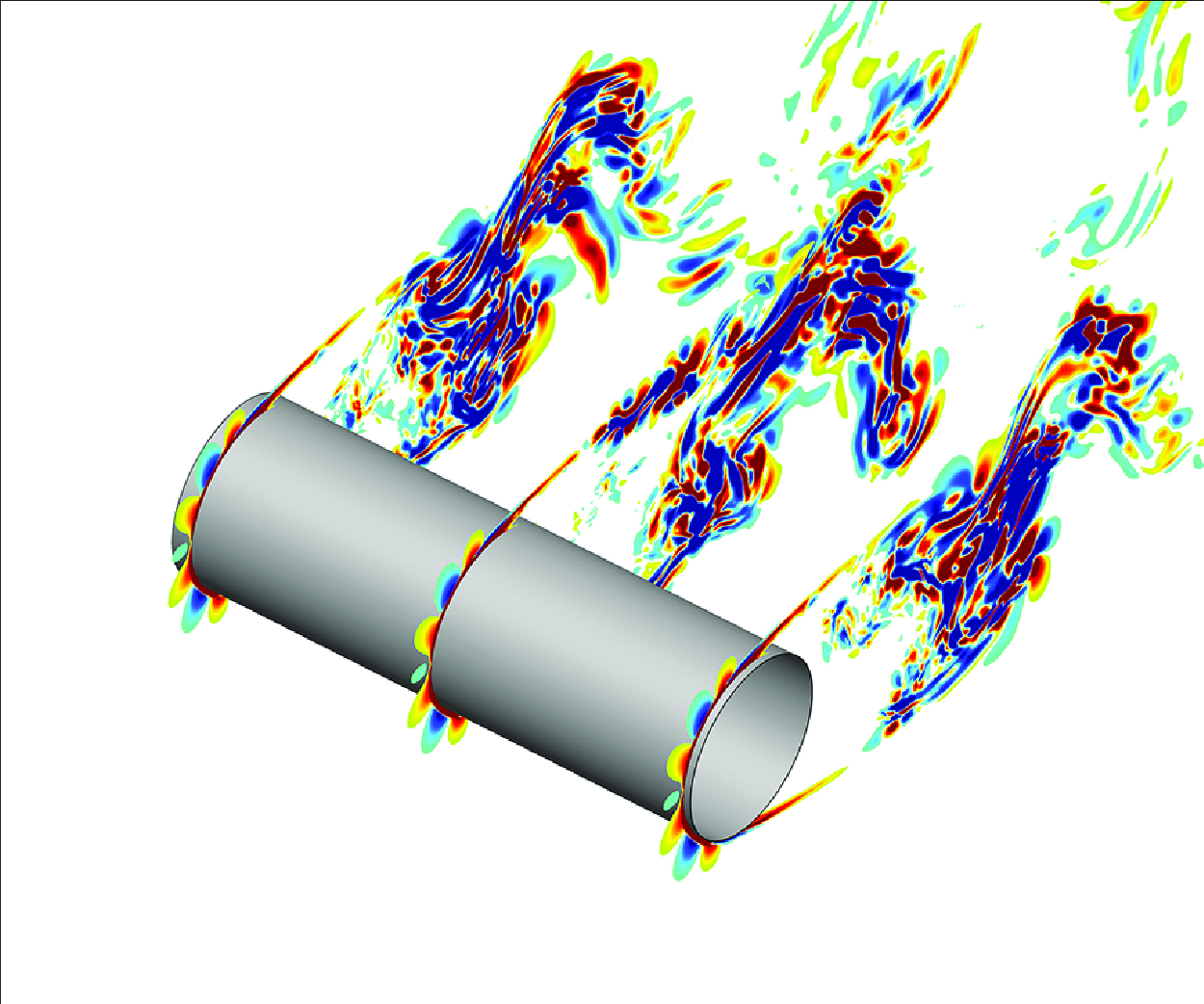
Noise source identification has been a long-standing challenge for decades. Although it is known that sound sources are closely related to flow structures, the underlying physical mechanisms remain controversial. This study develops a sound source identification method based on longitudinal and transverse process decomposition (LTD). Large-eddy simulations were performed on the flow around a cylinder at a Reynolds number of 3900. Using the new LTD method, sound sources in the cylinder flow were identified, and the mechanisms linking flow structures with noise generation were discussed in detail. Identifying the physical sound sources from two levels, low-order theory and high-order theory, the physical mechanism of wall sound sources was also analysed. Results indicate that the sound sources in the flow field mainly come from the leading edge, shear layer and wake region of the cylinder. The high-order theory reveals that sound sources are correlated with the spatio-temporal evolution of enstrophy, vortex stretching and surface deformation processes, this reflecting the coupling between transversal and longitudinal flow fields. The boundary thermodynamic flux and boundary dilatation flux distribution of the cylinder were analysed. Results indicate that the wall sound sources mainly come from the separation point and have a disorderly distribution on the leeward side of the cylinder, which is the main region where longitudinal variables enter the fluid from the wall surface, and the wall sound source is related to the boundary enstrophy flux.

JFM classification

Acoustics: Aeroacoustics Aerodynamics: Flow-structure interactions Turbulent Flows: Compressible turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1012 , 10 June 2025 , A13
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aguedal, L., Semmar, D., Berrouk, A.S., Azzi, A. & Oualli, H. 2018 3D Vortex structure investigation using large eddy simulation of flow around a rotary oscillating circular cylinder. Eur. J. Mech.-B/Fluids 71, 113–125.10.1016/j.euromechflu.2018.04.001CrossRefGoogle Scholar
Blevins, R.D. 1984 Review of sound induced by vortex shedding from cylinders. J. Sound Vib. 92 (4), 455–470.10.1016/0022-460X(84)90191-3CrossRefGoogle Scholar
Breuer, M. 1998 Large eddy simulation of the subcritical flow past a circular cylinder: numerical and modeling aspects. Intl J. Numer. Meth. Fluids 28 (9), 1281–1302.10.1002/(SICI)1097-0363(19981215)28:9<1281::AID-FLD759>3.0.CO;2-#3.0.CO;2-#>CrossRefGoogle Scholar
Chen, B-N., Yang, X-Q., Chen, G-Y., Tang, X-L., Ding, J. & Weng, P-F. 2022 a Numerical study on the flow and noise control mechanism of wavy cylinder. Phys. Fluids 34 (3), 036108.10.1063/5.0082896CrossRefGoogle Scholar
Chen, G-Y., Yang, X-Q., Tang, X-L., Ding, J. & Weng, P-F. 2022 b Effects of slat track on the flow and acoustic field of high-lift devices. Aerosp. Sci. Technol. 126, 107626.10.1016/j.ast.2022.107626CrossRefGoogle Scholar
Chen, G-Y., Tang, X-L., Yang, X-Q., Weng, P-F. & Ding, J. 2021 Noise control for high-lift devices by slat wall treatment. Aerosp. Sci. Technol. 115, 106820.10.1016/j.ast.2021.106820CrossRefGoogle Scholar
Chen, T., Wu, J.-Z., Liu, T. & Salazar, D.M. 2024 Boundary sources of velocity gradient tensor and its invariants. Phys. Fluids 36 (11), 117161.10.1063/5.0241226CrossRefGoogle Scholar
Chu, Y.-B. & Lu, X.-Y. 2013 Topological evolution in compressible turbulent boundary layers. J. Fluid Mech. 733, 414–438.10.1017/jfm.2013.399CrossRefGoogle Scholar
Colonius, T., Lele, S.K. & Moin, P. 1997 Sound generation in a mixing layer. J. Fluid Mech. 330, 375–409.10.1017/S0022112096003928CrossRefGoogle Scholar
Curle, N. 1955 The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. Lond. Series A. Math. Phys. Sci. 231 (1187), 505–514.Google Scholar
Dong, S., Karniadakis, G.E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207.10.1017/S0022112006002606CrossRefGoogle Scholar
Etkin, B., Korbacher, G.K. & Keefe, R.T. 1957 Acoustic radiation from a stationary cylinder in a fluid stream (Aeolian tones). J. Acoust. Soc. Am. 29 (1), 30–36.10.1121/1.1908673CrossRefGoogle Scholar
Feng, H-H., Chen, L. & Dong, Y-H. 2023 Modulation of wake evolution, separation, and radiated noise by a cylinder with porous media cladding. Phys. Fluids 35 (11), 115129.10.1063/5.0172352CrossRefGoogle Scholar
Ffowcs Williams, J.E. & Hawkings, D.L. 1969 Sound generation by turbulence and surfaces in arbitrary motion. Phil. Trans. R. Soc. Lond. Series A, Math. Phys. Sci. 264 (1151), 321–342.Google Scholar
Fröhlich, J., Rodi, W., Kessler, P., Parpais, S., Bertoglio, J.P. & Laurence, D. 1998 Large eddy simulation of flow around circular cylinders on structured and unstructured grids. Numerical Flow Simulation I: CNRS-DFG Collaborative Research Programme, Results 1996-1998. pp. 319–338.Google Scholar
Gerrard, J.H. 1955 Measurements of the sound from circular cylinders in an air stream. Proc. Phys. Soc. Section B 68 (7), 453–461.10.1088/0370-1301/68/7/307CrossRefGoogle Scholar
Goldstein, M.E. 2002 A unified approach to some recent developments in jet noise theory. Intl J. Aeroacoust. 1 (1), 1–16.10.1260/1475472021502640CrossRefGoogle Scholar
Hamman, C.W., Klewicki, J.C. & Kirby, R.M. 2008 On the Lamb vector divergence in Navier–Stokes flows. J. Fluid Mech. 610, 261–284.10.1017/S0022112008002760CrossRefGoogle Scholar
Howe, M.S. 1975 Contributions to the theory of aerodynamic sound, with application to excess jet noise and the theory of the flute. J. Fluid Mech. 71 (4), 625–673.10.1017/S0022112075002777CrossRefGoogle Scholar
Howe, M.S. 1998 Acoustics of Fluid-Structure Interactions. Cambridge University Press.10.1017/CBO9780511662898CrossRefGoogle Scholar
Howe, M.S. 2003 Theory of Vortex Sound. Cambridge University Press.Google Scholar
Inoue, O. & Hatakeyama, N. 2002 Sound generation by a two-dimensional circular cylinder in a uniform flow. J. Fluid Mech. 471, 285–314.10.1017/S0022112002002124CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.10.1017/S0022112095000462CrossRefGoogle Scholar
Kahil, Y. 2011 Large eddy simulation of the turbulent flows around circular cylinders at subcritical Reynolds number (ph. d. thesis). PhD thesis, Université Pierre et Marie Curie, Paris, France.Google Scholar
Kambe, T. 1986 Acoustic emissions by vortex motions. J. Fluid Mech. 173, 643–666.10.1017/S0022112086001301CrossRefGoogle Scholar
Kovasznay, L.S.G. 1953 Turbulence in supersonic flow. J. Aeronaut. Sci. 20 (10), 657–674.10.2514/8.2793CrossRefGoogle Scholar
Lagerstrom, P.A., Cole, J.D. & Trilling, L. 1949 Problems in the Theory of Viscous Compressible Fluids. California Institute of Technology Pasadena.Google Scholar
Li, S., Rival, D.E. & Wu, X. 2021 Sound source and pseudo-sound in the near field of a circular cylinder in subsonic conditions. J. Fluid Mech. 919, A43.10.1017/jfm.2021.404CrossRefGoogle Scholar
Lighthill, M.J. 1952 On sound generated aerodynamically i. general theory. Proc. R. Soc. Lond. Series A. Math. Phys. Sci. 211 (1107), 564–587.Google Scholar
Lilley, G.M. 1974 On the noise from jets. In Noise Mechanisms, AGARD-CP-131, pp. 13.1–13.12.Google Scholar
Lourenco, L.M. & Shih, C. 1994 Characteristics of the plane turbulent near wake of a circular cylinder, a particle image velocimetry study, numerical experiments on the flow past a circular cylinder at subcritical Reynolds Number. Tech. Rep. TF-62. Center for Turbulence Research, NASA Ames/Stanford University.Google Scholar
Ma, X., Karamanos, G.-S. & Karniadakis, G.E. 2000 Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 410, 29–65.10.1017/S0022112099007934CrossRefGoogle Scholar
Mao, F., Kang, L.L., Liu, L. & Wu, J.Z. 2022 a A unified theory for gas dynamics and aeroacoustics in viscous compressible flows. Part I. Unbounded fluid. Acta Mech. Sinica 38 (7), 321492.10.1007/s10409-022-09033-4CrossRefGoogle Scholar
Mao, F., Kang, L.L., Wu, J.Z., Yu, J.-L., Gao, A.K., Su, W.D. & Lu, X.-Y. 2020 A study of longitudinal processes and interactions in compressible viscous flows. J. Fluid Mech. 893, A23.10.1017/jfm.2020.213CrossRefGoogle Scholar
Mao, F., Liu, L.Q., Kang, L.L., Wu, J.Z., Zhang, P.J.Y. & Wan, Z.H. 2022 b A unified theory for gas dynamics and aeroacoustics in viscous compressible flows. Part II. Sources on solid boundary. Acta Mech. Sinica 38 (12), 321583.10.1007/s10409-022-21583-xCrossRefGoogle Scholar
Mao, F., Shi, Y.P., Xuan, L.J., Su, W.D. & Wu, J.Z. 2011 On the governing equations for the compressing process and its coupling with other processes. Sci. China Phys. Mech. Astron. 54 (6), 1154–1167.10.1007/s11433-011-4349-2CrossRefGoogle Scholar
Maryami, R. & Ali, S.A.S. 2023 Near-field pressure and wake velocity coherence of a circular cylinder. Phys. Fluids 35 (11), 115140.10.1063/5.0174931CrossRefGoogle Scholar
Maryami, R., Arcondoulis, E.J.G. & Liu, Y. 2024 Flow and aerodynamic noise control of a circular cylinder by local blowing. J. Fluid Mech. 980, A56.10.1017/jfm.2024.39CrossRefGoogle Scholar
Möhring, W., Müller, E.-A. & Obermeier, F. 1983 Problems in flow acoustics. Rev. Mod. Phys. 55 (3), 707–724.10.1103/RevModPhys.55.707CrossRefGoogle Scholar
Nicoud, F. & Ducros, F. 1999 Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 62 (3), 183–200.10.1023/A:1009995426001CrossRefGoogle Scholar
Norberg, C. 1998 Ldv-measurements in the near wake of a circular cylinder. ASME FEDSM98-5208. ASME Fluids Engineering Division — Summer Meeting, Advances in Understanding of Bluff Body wakes and Flow-Induced Vibration, American Society Of Mechanical Engineers (ASME).Google Scholar
Oguma, Y., Yamagata, T. & Fujisawa, N. 2013 Measurement of sound source distribution around a circular cylinder in a uniform flow by combined particle image velocimetry and microphone technique. J. Wind Engng Indust. Aerodyn. 118, 1–11.10.1016/j.jweia.2013.04.003CrossRefGoogle Scholar
Parnaudeau, P., Carlier, J., Heitz, D. & Lamballais, E. 2008 Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 20 (8), 085101.10.1063/1.2957018CrossRefGoogle Scholar
Phillips, O.M. 1960 On the generation of sound by supersonic turbulent shear layers. J. Fluid Mech. 9 (1), 1–28.10.1017/S0022112060000888CrossRefGoogle Scholar
Powell, A. 1964 Theory of vortex sound. J. Acoust. Soc. Am. 36 (1), 177–195.10.1121/1.1918931CrossRefGoogle Scholar
Pridmore-Brown, D.C. 1958 Sound propagation in a fluid flowing through an attenuating duct. J. Fluid Mech. 4 (4), 393–406.10.1017/S0022112058000537CrossRefGoogle Scholar
Tamura, A. & Tsutahara, M. 2010 Direct simulation of Aeolian tones emitted from a circular cylinder in transonic flows using the finite difference lattice Boltzmann method. Fluid Dyn. Res. 42 (1), 015007.10.1088/0169-5983/42/1/015007CrossRefGoogle Scholar
Truesdell, C. 2018 The kinematics of vorticity. Courier Dover Publications.Google Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2007 Vorticity and Vortex Dynamics. Springer Science & Business Media.Google Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2015 Vortical Flows. vol. 28. Springer.10.1007/978-3-662-47061-9CrossRefGoogle Scholar
Wu, T.Y.-t. 1956 Small perturbations in the unsteady flow of a compressible viscous and heat-conducting fluid. J. Maths Phys. 35 (1-4), 13–27.10.1002/sapm195635113CrossRefGoogle Scholar
Xu, C.-Y., Chen, L.-W. & Lu, X.-Y. 2010 Large-eddy simulation of the compressible flow past a wavy cylinder. J. Fluid Mech. 665, 238–273.10.1017/S0022112010003927CrossRefGoogle Scholar
Zhang, C., Moreau, S. & Sanjosé, M. 2019 Turbulent flow and noise sources on a circular cylinder in the critical regime. AIP Adv. 9 (8), 085009.10.1063/1.5121544CrossRefGoogle Scholar
Zhao, Q. 2018 Sound source localization of flow around circular cylinder by a virtual microphone array technique. AIP Adv. 8 (5), 055130.10.1063/1.5023457CrossRefGoogle Scholar