Hostname: page-component-84b7d79bbc-fnpn6 Total loading time: 0 Render date: 2024-07-27T10:09:50.616Z Has data issue: false hasContentIssue false
  • English
  • Français

The modification of turbulent thermal wind balance by non-traditional effects

Published online by Cambridge University Press:  25 August 2021

Matthew N. Crowe Open the ORCID record for Matthew N. Crowe [Opens in a new window]
Matthew N. Crowe*
Affiliation:
Department of Mathematics, University College London, London WC1E 6BT, UK
*
†Email address for correspondence: m.crowe@ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

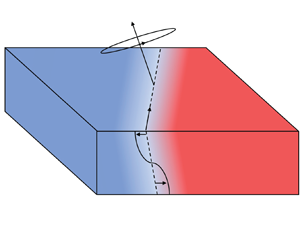
The meridional component of the earth's rotation is often neglected in geophysical contexts. This is referred to as the ‘traditional approximation’ and is justified by the typically small vertical velocity and aspect ratio of such problems. Ocean fronts are regions of strong horizontal buoyancy gradient and are associated with strong vertical transport of tracers and nutrients. Given these comparatively large vertical velocities, non-traditional rotation may play a role in governing frontal dynamics. Here the effects of non-traditional rotation on a front in turbulent thermal wind balance are considered using an asymptotic approach. Solutions are presented for a general horizontal buoyancy profile and examined in the simple case of a straight front. Non-traditional effects are found to depend strongly on the direction of the front and may lead to the generation of jets and the modification of the frontal circulation and vertical transport.

JFM classification

Geophysical and Geological Flows: Ocean circulation Geophysical and Geological Flows: Rotating flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 925 , 25 October 2021 , A17
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Blumen, W. 2000 Inertial oscillations and frontogenesis in a zero potential vorticity model. J. Phys. Oceanogr. 30, 31–39.2.0.CO;2>CrossRefGoogle Scholar
Burns, K.J., Vasil, G.M., Oishi, J.S., Lecoanet, D. & Brown, B.P. 2020 Dedalus: a flexible framework for numerical simulations with spectral methods. Phys. Rev. Res. 2, 023068.CrossRefGoogle Scholar
Charney, J.G. 1973 Symmetric circulations in idealized models. In Planetary Fluid Dynamics, pp. 128–141. D. Reidel Publishing Company.CrossRefGoogle Scholar
Coleman, G.N., Ferziger, J.H. & Spalart, P.R. 1990 A numerical study of the turbulent Ekman layer. J. Fluid Mech. 213, 313–348.CrossRefGoogle Scholar
Cronin, M.F. & Kessler, W.S. 2009 Near-surface shear flow in the tropical Pacific cold tongue front. J. Phys. Oceanogr. 39 (5), 1200–1215.CrossRefGoogle Scholar
Crowe, M.N. & Taylor, J.R. 2018 The evolution of a front in turbulent thermal wind balance, part 1. Theory. J. Fluid Mech. 850, 179–211.CrossRefGoogle Scholar
Crowe, M.N. & Taylor, J.R. 2019 a Baroclinic instability with a simple model for vertical mixing. J. Phys. Oceanogr. 49, 3273–3300.CrossRefGoogle Scholar
Crowe, M.N. & Taylor, J.R. 2019 b The evolution of a front in turbulent thermal wind balance, part 2. Numerical simulations. J. Fluid Mech. 880, 326–352.CrossRefGoogle Scholar
Crowe, M.N. & Taylor, J.R. 2020 The effects of surface wind stress and buoyancy flux on the evolution of a front in a turbulent thermal wind balance. Fluids 5 (2), 87.CrossRefGoogle Scholar
Eckart, C. 1960 Hydrodynamics of Oceans and Atmospheres, p. 290. Pergamon.Google Scholar
Eliassen, A. 1962 On the vertical circulation in frontal zones. Geofys. Publ. 24 (4), 147–160.Google Scholar
Ferrari, R. 2011 A frontal challenge for climate models. Science 332 (6027), 316–317.CrossRefGoogle ScholarPubMed
Garrett, C.J.R. & Loder, J.W. 1981 Dynamical aspects of shallow sea fronts. Phil. Trans. R. Soc. Lond. A 302, 563–581.Google Scholar
Garwood, R.W. 1991 Enhancements to deep turbulent entrainment. In Deep Convection and Deep Water Formation in the Oceans (ed. P.C. Chu & J.C. Gascard), Elsevier Oceanography Series, vol. 57, pp. 197–213. Elsevier.CrossRefGoogle Scholar
Gerkema, T. 2006 Internal-wave reflection from uniform slopes: higher harmonics and Coriolis effects. Nonlinear Process. Geophys. 13 (3), 265–273.CrossRefGoogle Scholar
Gerkema, T. & Shira, V.I. 2005 Near-inertial waves in the ocean: beyond the ‘traditional approximation’. J. Fluid Mech. 529, 195–219.CrossRefGoogle Scholar
Gerkema, T., Zimmerman, J.T.F., Maas, L.R.M. & van Haren, H. 2008 Geophysical and astrophysical fluid dynamics beyond the traditional approximation. Rev. Geophys. 46 (2), RG2004.CrossRefGoogle Scholar
Gula, J., Molemaker, M.J. & McWilliams, J.C. 2014 Submesoscale cold filaments in the Gulf Stream. J. Phys. Oceanogr. 44, 2617–2643.CrossRefGoogle Scholar
Hoskins, B.J. 1982 The mathematical theory of frontogenesis. Annu. Rev. Fluid Mech. 14, 131–151.CrossRefGoogle Scholar
Hoskins, B.J. & Bretherton, F.P. 1972 Atmospheric frontogenesis models: mathematical formulation and solution. J. Atmos. Sci. 29, 11–37.2.0.CO;2>CrossRefGoogle Scholar
Hua, B.L., Moore, D.W. & Gentil, S.L. 1997 Inertial nonlinear equilibration of equatorial flows. J. Fluid Mech. 331, 345–371.CrossRefGoogle Scholar
Lucas, C., McWilliams, J.C. & Rousseau, A. 2017 Large scale ocean models beyond the traditional approximation. Ann. Faculté Sci. Toulouse: Math. Ser. (6) 26 (4), 1029–1049.CrossRefGoogle Scholar
McWilliams, J.C. 2017 Submesoscale surface fronts and filaments: secondary circulation, buoyancy flux, and frontogenesis. J. Fluid Mech. 823, 391–432.CrossRefGoogle Scholar
McWilliams, J.C., Gula, J., Molemaker, M.J., Renault, L. & Shchepetkin, A.F. 2015 Filament frontogenesis by boundary layer turbulence. J. Phys. Oceanogr. 45, 1988–2005.CrossRefGoogle Scholar
McWilliams, J.C. & Huckle, E. 2006 Ekman layer rectification. J. Phys. Oceanogr. 36 (8), 1646–1659.CrossRefGoogle Scholar
Orlanski, I. & Ross, B.B. 1977 The circulation associated with a cold front: part I: dry case. J. Atmos. Sci. 34, 1619–1633.2.0.CO;2>CrossRefGoogle Scholar
Shakespeare, C.J. & Taylor, J.R. 2013 A generalized mathematical model of geostrophic adjustment and frontogenesis: uniform potential vorticity. J. Fluid Mech. 736, 366–413.CrossRefGoogle Scholar
Sheremet, V.A. 2004 Laboratory experiments with tilted convective plumes on a centrifuge: a finite angle between the buoyancy force and the axis of rotation. J. Fluid Mech. 506, 217–244.CrossRefGoogle Scholar
Stone, P.H. 1966 On non-geostrophic baroclinic stability. J. Atmos. Sci. 23, 390–400.2.0.CO;2>CrossRefGoogle Scholar
de Verdière, A.C. & Schopp, R. 1994 Flows in a rotating spherical shell: the equatorial case. J. Fluid Mech. 276, 233–260.CrossRefGoogle Scholar
Wenegrat, J.O. & McPhaden, M.J. 2016 Wind, waves, and fronts: frictional effects in a generalized Ekman model. J. Phys. Oceanogr. 46 (2), 371–394.CrossRefGoogle Scholar
Wenegrat, J.O. & Thomas, L.N. 2017 Ekman transport in balanced currents with curvature. J. Phys. Oceanogr. 47 (5), 1189–1203.CrossRefGoogle Scholar