Article contents
Motion of a tightly fitting axisymmetric object through a lubricated elastic tube
Published online by Cambridge University Press: 10 September 2021
Abstract
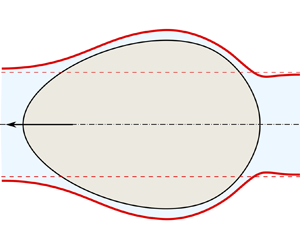
We consider the translation of a rigid, axisymmetric, tightly fitting object through a cylindrical elastic tube filled with viscous fluid, using a combination of theory and direct numerical simulations. The intruding object is assumed to be wider than the undeformed tube radius, forcing solid–solid contact in the absence of relative motion. The motion of the object establishes a thin fluid film that lubricates this contact. Our theory couples lubrication theory to a geometrically nonlinear membrane description of the tube's elasticity, and applies to a slender intruding object and a thin tube with negligible bending rigidity. We show using asymptotic and numerical solutions of the theory, that the thickness of the thin fluid film scales with the square root of the relative speed for small speeds, set by a balance of hoop stresses, membrane tension and fluid pressure. While membrane tension is relatively small at the entrance of the film, it dominates near the exit and produces undulations of the film thickness, even in the limit of vanishing speeds and slender objects. We find that the drag force on the intruding object depends on the slope of its surface at the entrance to the thin fluid film, and scales as the square root of the relative speed. The predictions of the lubricated membrane theory for the shape of the film and the force on the intruder are in quantitative agreement with three-dimensional direct numerical simulations of the coupled fluid–elastic problem.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by


