Hostname: page-component-5db6c4db9b-wnbrb Total loading time: 0 Render date: 2023-03-25T18:16:54.814Z Has data issue: true Feature Flags: { "useRatesEcommerce": false } hasContentIssue true
  • English

A multifold reduction in the transition Reynolds number, and ultra-fast mixing, in a micro-channel due to a dynamical instability induced by a soft wall

Published online by Cambridge University Press:  26 June 2013

M. K. S. Verma  and
V. Kumaran
M. K. S. Verma
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
V. Kumaran*
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
*
†Email address for correspondence: kumaran@chemeng.iisc.ernet.in
Get access Rights & Permissions[Opens in a new window]

Abstract

A dynamical instability is observed in experimental studies on micro-channels of rectangular cross-section with smallest dimension 100 and 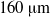$160~\mathrm{\mu} \mathrm{m} $ in which one of the walls is made of soft gel. There is a spontaneous transition from an ordered, laminar flow to a chaotic and highly mixed flow state when the Reynolds number increases beyond a critical value. The critical Reynolds number, which decreases as the elasticity modulus of the soft wall is reduced, is as low as 200 for the softest wall used here (in contrast to 1200 for a rigid-walled channel). The instability onset is observed by the breakup of a dye-stream introduced in the centre of the micro-channel, as well as the onset of wall oscillations due to laser scattering from fluorescent beads embedded in the wall of the channel. The mixing time across a channel of width 1.5 mm, measured by dye-stream and outlet conductance experiments, is smaller by a factor of 105 than that for a laminar flow. The increased mixing rate comes at very little cost, because the pressure drop (energy requirement to drive the flow) increases continuously and modestly at transition. The deformed shape is reconstructed numerically, and computational fluid dynamics (CFD) simulations are carried out to obtain the pressure gradient and the velocity fields for different flow rates. The pressure difference across the channel predicted by simulations is in agreement with the experiments (within experimental errors) for flow rates where the dye stream is laminar, but the experimental pressure difference is higher than the simulation prediction after dye-stream breakup. A linear stability analysis is carried out using the parallel-flow approximation, in which the wall is modelled as a neo-Hookean elastic solid, and the simulation results for the mean velocity and pressure gradient from the CFD simulations are used as inputs. The stability analysis accurately predicts the Reynolds number (based on flow rate) at which an instability is observed in the dye stream, and it also predicts that the instability first takes place at the downstream converging section of the channel, and not at the upstream diverging section. The stability analysis also indicates that the destabilization is due to the modification of the flow and the local pressure gradient due to the wall deformation; if we assume a parabolic velocity profile with the pressure gradient given by the plane Poiseuille law, the flow is always found to be stable.

JFM classification

Instability: Instability Micro-/Nano-fluid dynamics: Microfluidics Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 727 , 25 July 2013 , pp. 407 - 455
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, D., Mao, X., Shi, J., Juluri, B. & Huang, T. 2009 A millisecond micromixer via single-bubble-based acoustic streaming. Lab on a Chip 9, 2738–2741.CrossRefGoogle ScholarPubMed
Bazant, M. Z. & Squires, T. M. 2004 Induced-charge electro-kinetic phenomena: theory and microfluidic applications. Phys. Rev. Lett. 92, 066101.CrossRefGoogle Scholar
Bessoth, F., de Mello, A. J. & Manz, A. 1999 Microstructure for efficient continuous flow mixing. Anal. Commun. 36, 213–215.CrossRefGoogle Scholar
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 2007 Transport Phenomena. John Wiley & Sons.Google Scholar
Boyd, J. P. 1989 Chebyshev and Fourier Spectral Methods. Springer.CrossRefGoogle Scholar
Chokshi, P. P. & Kumaran, V. 2008 Weakly nonlinear analysis of viscous instability in flow past a neo-Hookean surface. Phys. Rev. E 77, 056303.CrossRefGoogle Scholar
Chokshi, P. P. & Kumaran, V. 2009 Weakly nonlinear stability analysis of a flow past a neo-Hookean solid at arbitrary Reynolds numbers. Phys. Fluids 21, 014109.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
Eggert, M. D. & Kumar, S. 2004 Observations of instability, hysteresis, and oscillation in low-Reynolds-number flow past polymer gels. J. Colloid Interface Sci. 278, 234–242.CrossRefGoogle ScholarPubMed
Ganan-Calvo, A. M., Ferrera, C., Torregrosa, M., Herrada, M. A. & Marchand, M. 2011 Experimental and numerical study of the recirculation flow inside a liquid meniscus focused by air. Microfluid Nanofluid 11, 65–74.CrossRefGoogle Scholar
Gaster, M. 1962 A note on the relation between temporally-increasing and spatially-increasing disturbances in hydrodynamic stability. J. Fluid Mech. 14, 222–224.CrossRefGoogle Scholar
Gaurav, & Shankar, V. 2009 Stability of fluid flow through deformable neo-Hookean tubes. J. Fluid Mech. 627, 291–322.CrossRefGoogle Scholar
Gaurav, & Shankar, V. 2010 Stability of pressure-driven flow in a deformable neo-Hookean channel. J. Fluid Mech. 659, 318–350.CrossRefGoogle Scholar
Gervais, T., El-Ali, J., Guntherb, A. & Jensen, K. F. 2006 Flow-induced deformation of shallow microfluidic channels. Lab on a Chip 6, 500–507.CrossRefGoogle ScholarPubMed
Gkanis, V. & Kumar, S. 2005 Stability of pressure driven creeping flows in channels lined with a nonlinear elastic solid. J. Fluid Mech. 524, 357–375.CrossRefGoogle Scholar
Glasgow, I. & Aubry, N. 2003 Enhancement of microfluidic mixing using time pulsing. Lab on a Chip 3, 114–116.CrossRefGoogle ScholarPubMed
Gordillo, J. M., Cheng, Z., Ganan-Calvo, A. M., Marquez, M. & Weitz, D. A. 2004 A new device for the generation of microbubbles. Phys. Fluids 16, 2828–2834.CrossRefGoogle Scholar
Hardy, B. S., Uechi, K., Zhen, J. & Kavehpour, H. P. 2009 The deformation of flexible PDMS microchannels under a pressure driven flow. Lab on a Chip 9, 935–938.CrossRefGoogle Scholar
Hof, B., Juel, A. & Mullin, T. 2003 Scaling of the turbulence transition threshold in a pipe. Phys. Rev. Lett. 91, 244502.CrossRefGoogle Scholar
Jiang, F., Drese, K. S., Hardt, S., Kupper, M. & Schonfeld, F. 2004 Helical flows and chaotic mixing in curved micro channels. AIChE J. 50, 2297–2305.CrossRefGoogle Scholar
Kane, A. S., Hoffmann, A., Baumgartel, P., Seckler, R., Reichardt, G., Horsley, D. A., Schuler, B. & Bakajin, O. 2008 Microfluidic mixers for the investigation of rapid protein folding kinetics using synchrotron radiation circular dichroism spectroscopy. Analyt. Chem. 80, 9534–9541.CrossRefGoogle ScholarPubMed
Knight, J. B., Vishwanath, A., Brody, J. P. & Austin, R. H. 1998 Hydrodynamic focusing on a silicon chip: mixing nanoliters in microseconds. Phys. Rev. Lett. 80, 3863–3866.CrossRefGoogle Scholar
Krindel, P. & Silberberg, A. 1979 Flow through gel-walled tubes. J. Colloid Interface Sci. 71, 39–50.CrossRefGoogle Scholar
Kumaran, V. 1995 Stability of the viscous flow of a fluid through a flexible tube. J. Fluid Mech. 294, 259–281.CrossRefGoogle Scholar
Kumaran, V. 1996 Stability of an inviscid flow in a flexible tube. J. Fluid Mech. 320, 1–17.CrossRefGoogle Scholar
Kumaran, V. 1998 Stability of fluid flow in a flexible tube at intermediate Reynolds number. J. Fluid Mech. 357, 123–140.CrossRefGoogle Scholar
Kumaran, V., Fredrickson, G. H. & Pincus, P. 1994 Flow induced instability at the interface between a fluid and a gel at low Reynolds number. J. Phys. France II 4, 893–911.CrossRefGoogle Scholar
Kumaran, V. & Muralikrishnan, R. 2000 Spontaneous growth of fluctuations in the viscous flow of a fluid past a soft interface. Phys. Rev. Lett. 84, 3310–3313.CrossRefGoogle Scholar
Lee, M. G., Choi, S. & Park, J.-K. 2010 Rapid multivortex mixing in an alternately formed contraction-expansion array microchannel. Biomed. Microdevices 12, 1019–1026.CrossRefGoogle Scholar
Lee, S., Kim, D., Lee, S. & Kwon, T 2006 A split and recombination micromixer fabricated in a PDMS three-dimensional structure. J. Micromech. Microengng 16, 1067–1074.CrossRefGoogle Scholar
Liu, R. H., Stremler, M. A., Sharp, K. V., Olsen, M. G., Santiago, J. G., Adrian, R. J., Aref, H. & Beebe, D. J. 2000 Passive mixing in a three-dimensional serpentine microchannel. J. Microelectromech. Syst. 9, 190–197.CrossRefGoogle Scholar
Mensing, G. A., Pearce, T. M., Graham, M. D. & Beebe, D. J. 2004 An externally driven magnetic micro-stirrer. Phil. Trans. R. Soc. Lond. A 362, 1059–1068.CrossRefGoogle Scholar
Muralikrishnan, R. & Kumaran, V. 2002 Experimental study of the instability of the viscous flow past a flexible surface. Phys. Fluids 14, 775–780.CrossRefGoogle Scholar
Posner, J. & Santiago, J. J. 2006 Convective instability of electrokinetic flows in a cross-shaped microchannel. J. Fluid Mech. 555, 1–42.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 1994 Optimal energy density growth in Hagen-Poiseuille flow. J. Fluid Mech. 277, 197–225.CrossRefGoogle Scholar
Shankar, V. & Kumaran, V. 1999 Stability of non-parabolic flows in a flexible tube. J. Fluid Mech. 395, 211–236.CrossRefGoogle Scholar
Shankar, V. & Kumaran, V. 2000 Stability of non-axisymmetric modes in a flexible tube. J. Fluid Mech. 407, 291–314.CrossRefGoogle Scholar
Shankar, V. & Kumaran, V. 2001a Asymptotic analysis of wall modes in a flexible tube revisited. Eur. Phys. J. B 19, 607–622.CrossRefGoogle Scholar
Shankar, V. & Kumaran, V. 2001b Weakly nonlinear stability of viscous flow past a flexible surface. J. Fluid Mech. 434, 337–354.CrossRefGoogle Scholar
Shankar, V. & Kumaran, V. 2002 Stability of wall modes in the flow past a flexible surface. Phys. Fluids 14, 2324–2338.CrossRefGoogle Scholar
Shrivastava, A., Cussler, E. L. & Kumar, S. 2008 Mass transfer enhancement due to a soft elastic boundary. Chem. Engng Sci. 63, 4302–4305.CrossRefGoogle Scholar
Stroock, A. D., Dertinger, S. K. W., Ajdari, A., Mezic, I., Stone, H. A. & Whitesides, G. M. 2002 Chaotic mixer for microchannels. Nature 295, 647–651.Google ScholarPubMed
Sutterby, J. L. 1965 Finite difference analysis of viscous laminar converging flow in conical tubes. Appl. Sci. Res. A 15, 241–252.CrossRefGoogle Scholar
Thaokar, R. M., Shankar, V. & Kumaran, V. 2001 Effect of tangential interface motion on the viscous instability in fluid flow past flexible surfaces. Eur. Phys. J. B 23, 533–550.CrossRefGoogle Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.CrossRefGoogle ScholarPubMed
Verma, M. K. S. & Kumaran, V. 2012 A dynamical instability due to fluid-wall coupling lowers the transition Reynolds number in the flow through a flexible tube. J. Fluid Mech. 705, 322–347 2012.CrossRefGoogle Scholar
Weideman, J. A. & Reddy, S. C. 2000 A Matlab differentiation matrix suite. ACM Trans. Math. Softw. 26, 465519.CrossRefGoogle Scholar
Yang, C., Grattoni, C. A., Muggeridge, A. H. & Zimmerman, R. W. 2000 A model for steady laminar flow through a deformable gel-coated channel. J. Colloid. Interface Sci. 266, 104–111.Google Scholar