Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T18:41:31.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal stresses in concentrated non-Brownian suspensions

Published online by Cambridge University Press:  09 January 2013

T. Dbouk ,
L. Lobry  and
E. Lemaire
T. Dbouk
Affiliation:
Laboratoire de Physique de la Matière Condensée (LPMC, UMR 6622), Parc Valrose, 06108 Nice CEDEX 2
L. Lobry
Affiliation:
Laboratoire de Physique de la Matière Condensée (LPMC, UMR 6622), Parc Valrose, 06108 Nice CEDEX 2
E. Lemaire*
Affiliation:
Laboratoire de Physique de la Matière Condensée (LPMC, UMR 6622), Parc Valrose, 06108 Nice CEDEX 2
*
†Email address for correspondence: elemaire@unice.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an experimental approach used to measure both normal stress differences and the particle phase contribution to the normal stresses in suspensions of non-Brownian hard spheres. The methodology consists of measuring the radial profile of the normal stress along the velocity gradient direction in a torsional flow between two parallel discs. 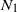The values of the first and the second normal stress differences, ${N}_{1} $ and 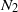${N}_{2} $, are deduced from the measurement of the slope and of the origin ordinate. The measurements are carried out for a wide range of particle volume fractions (between 0.2 and 0.5). As expected, 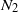${N}_{2} $ is measured to be negative but 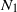${N}_{1} $ is found to be positive. We discuss the validity of the method and present numerous tests that have been carried out in order to validate our results. The experimental setup also allows the pore pressure to be measured. Then, subtracting the pore pressure from the total stress, 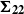${\mbrm{\Sigma} }_{\mathbf{22} } $, the contribution of the particles to the normal stress 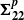${ \mbrm{\Sigma} }_{\mathbf{22} }^{\mathbi{p}} $ is obtained. Most of our results compare well with the different experimental and numerical data present in the literature. In particular, our results show that the magnitude of the particle stress tensor component and their dependence on the particle volume fraction used in the suspension model balance proposed by Morris & Boulay (J. Rheol., vol. 43, 1999, p. 1213) are suitable.

JFM classification

Non-Newtonian Flows: Non-Newtonian Flows Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 239 - 272
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A., Mauri, R. & Fan, X. 1993 Shear-induced resuspension in a Couette device. Intl J. Multiphase Flow 19, 797.CrossRefGoogle Scholar
Bird, R. B., Armstrong, R. C. & Hassager, O. 1977 Dynamics of polymeric liquids. In Fluid Mechanics, vol. 1. John Wiley & sons.Google Scholar
Blanc, F. 2011 Rhéologie et microstructure des suspensions concentres non-Browniennes. PhD thesis, Université de Nice.Google Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011a Local transient rheological behaviour of concentrated suspensions. J. Rheol. 55, 835.CrossRefGoogle Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011b Experimental signature of the pair trajectories of rough spheres in the shear-induced microstructure in noncolloidal suspensions. Phys. Rev. Lett. 107, 208302.CrossRefGoogle ScholarPubMed
Boyer, F., Pouliquen, O. & Guazzelli, E. 2011a Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5.Google Scholar
Boyer, F., Guazzelli, E. & Pouliquen, O. 2011b Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.CrossRefGoogle ScholarPubMed
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 103.Google Scholar
Bricker, J. M. & Butler, J. E. 2006 Oscillatory shear of suspensions of noncolloidal particles. J. Rheol. 50, 711.Google Scholar
Chapman, B. 1990 Shear-induced migration phenomena in concentrated suspensions. PhD thesis, University of Notre Dame.Google Scholar
Chow, A. W., Iwayima, J. H., Sinton, S. W. & Leighton, D. T. 1995 Particle migration of non-Brownian, concentrated suspensions in a truncated cone-and-plate. Society of Rheology Meeting, Sacramento, CA.Google Scholar
Chow, A. W., Sinton, S. W., Iwamiya, J. H. & Stephens, T. S. 1994 Shear-induced migration in Couette and parallel-plate viscometers: NMR imaging and stress measurements. Phys. Fluids 6, 2561.Google Scholar
Couturier, E., Boyer, F., Pouliquen, O. & Guazzelli, E. 2011 Suspensions in a tilted trough: second normal stress difference. J. Fluid Mech. 686, 26.Google Scholar
Deboeuf, A. 2008 Interactions hydrodynamiques dans les suspensions macroscopiques. PhD thesis, Université Pierre & Marie Curie.Google Scholar
Deboeuf, A., Gauthier, G., Martin, J., Yurkovetsky, Y. & Morris, J. F. 2009 Particle pressure in a sheared suspension: a Bbridge from osmosis to granular dilatancy. Phys. Rev. Lett. 102, 108301.Google Scholar
Gadala-Maria, F. 1979 The rheology of concentrated suspensions. PhD thesis, Stanford University.Google Scholar
Gadala-Maria, F. & Acrivos, A. 1980 Shear-induced structure in a concentrated suspension of solid spheres. J. Rheol. 24, 799.Google Scholar
Guyon, E., Hulin, J. P. & Petit, L. 2001 Hydrodynamique Physique. Savoirs Actuels, EDP Sciences/CNRS editions.Google Scholar
Jana, S. C, Kapoor, B. & Acrivos, A. 1995 Apparent wall slip velocity coefficients in concentrated suspensions of non colloidal particles. J. Rheol. 39, 1123.Google Scholar
Keentok, M. V. & Xue, S. C. 1999 Edge fracture in cone-plate and parallel plate flows. Rheol. Acta 38, 321.CrossRefGoogle Scholar
Kim, J. M., Lee, S. G. & Kim, D. C. 2008 Numerical simulations of particle migration in suspension flows: frame-invariant formulation of curvature-induced migration. J. Non-Newtonian Fluid Mech. 150, 162.Google Scholar
Lhuillier, D. 2009 Migration of rigid particles in non-Brownian viscous suspensions. Phys. Fluids 21, 023302.Google Scholar
Mccoy, D. H. & Denn, M. M. 1971 Secondary flow in a parallel plate rheometer. Rheol. Acta 10, 408.Google Scholar
Merhi, D., Lemaire, E., Bossis, G. & Moukalled, F. 2005 Particle migration in a concentrated suspension flowing between rotating parallel plates: investigation of diffusion flux coefficients. J. Rheol. 49, 1429.CrossRefGoogle Scholar
Mills, P. & Snabre, P. 1995 Rheology and structure of concentrated suspensions of hard spheres. Shear induced particle migration. J. Phys. II France 5, 1597.Google Scholar
Mills, P. & Snabre, P. 2009 Apparent viscosity and particle pressure of a concentrated suspension of non-Brownian hard spheres near the jamming transition. Eur. Phys. J. E 30, 309.CrossRefGoogle ScholarPubMed
Morris, J. F. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J. Rheol. 43 (5), 1213.CrossRefGoogle Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157.Google Scholar
Nott, P. R., Guazzelli, E. & Pouliquen, O. 2011 The suspension balance model revisited. Phys. Fluids 23, 043304.Google Scholar
Ovarlez, G., Bertrand, F. & Rodts, S. 2006 Local determination of the constitutive law of a dense suspension of noncolloidal particles through magnetic resonance imaging. J. Rheol. 50, 259.Google Scholar
Parsi, F. & Gadala-Maria, F. 1987 Fore-and-aft asymmetry in a concentrated suspension of solid spheres. J. Rheol. 31, 725.Google Scholar
Phillips, R. J., Armstrong, R. C., Brown, R. A., Graham, A. & Abbott, J. R. 1992 A constitutive model for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A 4, 30.Google Scholar
Phung, T. N., Brady, J. F. & Bossis, G. 1996 Stokesian dynamics simulations of Brownian suspensions. J. Fluid Mech. 313, 181.Google Scholar
Prasad, D. & Kytomaa, H. 1995 Particle stress and viscous compaction during shear of dense suspensions. Intl J. Multiphase Flow 21 (5), 775.Google Scholar
Ramachandran, A. & Leigton, D. T. 2010 Particle migration in concentrated suspensions undergoing squeeze flow. J. Rheol. 54, 563.Google Scholar
Richardson, J. F. & Zaki, W. N. 1954 Sedimentation and fluidization. Part I. Trans. Inst. Chem. Engng 32, 35.Google Scholar
Sierrou, A. & Brady, J. F. 2002 Rheology and microstructure in concentrated noncolloidal suspensions. J. Rheol. 46, 1031.Google Scholar
Singh, A. & Nott, P. R. 2003 Experimental measurements of the normal stresses in sheared Stokesian suspensions. J. Fluid Mech. 490, 293.Google Scholar
Stickel, J. J. & Powell, R. L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129.Google Scholar
Tanner, R. I. & Pipkin, A. C. 1969 Intrinsic errors in pressure-hole measurements. Trans. Soc. Rheol. 13, 471.Google Scholar
Yeo, K. & Maxey, M. R. 2010 Dynamics of concentrated suspensions of non-colloidal particles in Couette flow. J. Fluid Mech. 649, 205.Google Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 44, 185.Google Scholar