Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-22T01:34:28.888Z Has data issue: false hasContentIssue false
  • English
  • Français

A numerical investigation of the turbulent Stokes–Ekman bottom boundary layer

Published online by Cambridge University Press:  06 September 2011

S. Salon  and
V. Armenio
S. Salon
Affiliation:
OGS (Istituto Nazionale di Oceanografia e di Geofisica Sperimentale), Sgonico (TS), Italy
V. Armenio*
Affiliation:
Dipartimento di Ingegneria Civile e Ambientale, Università degli Studi di Trieste, Piazzale Europa 1, 34127 Trieste, Italy
*
†Email address for correspondence: armenio@dic.units.it
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present paper turbulent mixing in the Stokes–Ekman bottom boundary layer is investigated analytically and by wall-resolving large-eddy simulations (LES). The analytical solution shows that when the Rossby number oscillation and rotation interact with each other, this gives rise to a thickening of the boundary layer compared with the purely oscillating or the purely rotating case. The solution also shows the presence of elliptical patterns developing on the horizontal planes that shrink when approaching the low latitudes. In the turbulent regime, a LES was applied for an east–west tidal current, considered at three different latitudes in the Northern Hemisphere, namely, the polar case, the mid-latitude case (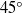) and the quasi-equatorial case (). The Reynolds number of the simulation, based on the viscous penetration depth and the frequency of the purely oscillatory flow, was set equal to . The analysis suggests that rotation has two main effects on the flow field: in the polar case, rotation tends to delay the cyclic re-transition to turbulence and to narrow the turbulent phases of the cycle. Also, rotation suppresses vertical fluctuations of velocity and redistributes energy from the streamwise direction to the spanwise direction. It is noteworthy that the high-latitude effect makes the turbulent field substantially different from the reference Stokes boundary layer case, whereas the low-latitude effects appear to be of secondary importance, owing to the weakness of the rotation rate. Consequently, the study shows that the Stokes boundary layer may be representative of the oceanic bottom boundary layer in the low-latitude cases ( cases in our simulations). Conversely, it cannot be considered as archetypal of the oceanic boundary layer at high latitudes ( case of our study), where the vertical background vorticity profoundly modifies the turbulent field.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulence simulation Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 684 , 10 October 2011 , pp. 316 - 352
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Aelbrecht, D., Chabert D’Hieres, G. & Renouard, D. 1999 A 3-D coastal tidal rectification process: observations, theory and experiments. Cont. Shelf Res. 19, 1869–1903.CrossRefGoogle Scholar
2. Armenio, V. & Piomelli, U. 2000 A Lagrangian mixed subgrid-scale model in generalized coordinates. Flow Turbul. Combust. 65, 51.CrossRefGoogle Scholar
3. Armenio, V. & Sarkar, S. 2004 Mixing in a stably-stratified medium by horizontal shear near vertical walls. Theor. Comput. Fluid Dyn. 17 (5–6).Google Scholar
4. Bardina, J., Ferziger, J. H. & Reynolds, W. C. 1980 Improved subgrid scale models for large eddy simulation. AIAA paper (80–1357).CrossRefGoogle Scholar
5. Bartello, P., Metais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273, 1–29.CrossRefGoogle Scholar
6. Book, J. W., Martin, P. J, Janekoviĉ, I., Kuzmiĉ, M. & Wimbush, M. 2009 Vertical structure of bottom Ekman tidal flows: observations, theory, and modeling from the northern adriatic. J. Geophys. Res. 114, C01S06.Google Scholar
7. Bradshaw, P. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36, 177.Google Scholar
8. Cambon, C., Benoit, J.-P., Shao, L. & Jacquin, L. 1994 Stability analysis and large-eddy simulation of rotating turbulence with oranized eddies. J. Fluid Mech. 278, 175–200.CrossRefGoogle Scholar
9. Cartwright, D. E. & Ray, R. D. 1991 Energetics of global ocean tides from Geosat altimetry. J. Geophys. Res. 96 (C9), 16897.CrossRefGoogle Scholar
10. Coleman, G. N. 1999 Similarity statistics from a direct numerical simulation of the neutrally stratified planetary boundary layer. J. Atmos. Sci. 56 (6), 891–900.Google Scholar
11. Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1990 A numerical study of the turbulent Ekman layer. J. Fluid Mech. 213, 313–348.CrossRefGoogle Scholar
12. Cui, A. & Street, R. L. 2004 Large-eddy simulation of coastal upwelling flow. Environ. Fluid Mech. 4, 197–223.Google Scholar
13. Esau, I. N. 2003 The Coriolis effect on coherent structures in planetary boundary layers. J. Turbul. 4, 017.CrossRefGoogle Scholar
14. Esau, I. N. 2004 Simulation of Ekman boundary layers by large eddy model with dynamic mixed subfilter closure. Environ. Fluid Mech. 4, 273–303.Google Scholar
15. Etling, D. & Wippermann, F. 1975 On the instability of a planetary boundary layer with Rossby-number similarity. Boundary-Layer Meteorol. 9, 341–360.CrossRefGoogle Scholar
16. Falcomer, L. & Armenio, V. 2002 Large-eddy simulation of secondary flow over longitudinally-ridged walls. J. Turbul. 1, 011.Google Scholar
17. Furevik, T. & Foldvik, A. 1996 Stability at M 2 critical latitude in the Barents sea. J. Geophys. Res. 101 (C4), 8823–8837.CrossRefGoogle Scholar
18. Greenblatt, D. & Moss, E. 2004 Rapid temporal acceleration of a turbulent pipe flow. J. Fluid Mech. 514, 65.Google Scholar
19. Hopfinger, E. J. & Linden, P. F. 1990 The effect of background rotation on fluid motions: a report on Euromech 245. J. Fluid Mech. 211, 417–435.Google Scholar
20. Jensen, B. L., Sumer, B. M. & Fredsøe, J. 1989 Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 206, 265.Google Scholar
21. Johnston, J. P., Halleen, R. M. & Lezius, D. K. 1972 Effects of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56, 533–557.Google Scholar
22. Kristoffersen, R. & Andersson, H. I. 1993 Direct simulations of low-Reynolds-number turbulent flow in a rotating channel. J. Fluid Mech. 256, 163.CrossRefGoogle Scholar
23. Leibovich, S. & Lele, S. K. 1985 The influence of the horizontal component of Earth’s angular velocity on the instability of the Ekman layer. J. Fluid Mech. 150, 41–87.Google Scholar
24. Lu, Y., Lueck, R. G. & Huang, D. 2000 Turbulence characteristics in a tidal channel. J. Phys. Oceanogr. 30, 855–867.Google Scholar
25. Maas, L. R. M. & van Haren, J. J. M. 1987 Observations on the vertical structure of tidal and inertial currents in the central North Sea. J. Mar. Res. 45, 293–318.Google Scholar
26. Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539.Google Scholar
27. Munk, W., Snodgrass, F. & Wimbush, M. 1970 Tides offshore: transition from California coastal to deep-sea water. Geophys. Fluid Dyn. 1, 161–235.CrossRefGoogle Scholar
28. Narasimha, R. & Sreenivasan, K. R. 1973 Relaminarization in higly accelerated turbulent boundary layers. J. Fluid Mech. 61, 417.Google Scholar
29. Piomelli, U. & Liu, J. 1995 Large-eddy simulation of rotating channel flows using a localized dynamic model. Phys. Fluids 7, 839.CrossRefGoogle Scholar
30. Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
31. Prandle, D. 1982 The vertical structure of tidal currents and other oscillatory flows. Cont. Shelf Res. 1, 191–207.Google Scholar
32. Sakamoto, K. & Akitomo, K. 2008 The tidally induced bottom boundary layer in a rotating frame: similarity of turbulence. J. Fluid Mech. 615, 1–25.CrossRefGoogle Scholar
33. Salon, S., Armenio, V. & Crise, A. 2007 A numerical investigation of the Stokes boundary layer in the turbulent regime. J. Fluid Mech. 570, 253–296.Google Scholar
34. Salon, S., Armenio, V. & Crise, A. 2009 A numerical (LES) investigation of a shallow-water, mid-latitude, tidally-driven boundary layer. Environ. Fluid Mech., 9 (5), 525–547 doi:10.1007/s10652-009-9122-y.Google Scholar
35. Sanford, T. B. & Lien, R. C. 1999 Turbulent properties in a homogenaous tidal bottom boundary layer. J. Geophys. Res. 104 (C1), 1245–1257.CrossRefGoogle Scholar
36. Smagorinsky, J. 1963 General circulation experiments with the primitive equations. I. The basic experiment. Mon. Weath. Rev. 91, 99.Google Scholar
37. Soulsby, R. L. 1983 The bottom boundary layer of shelf seas. In Physical Oceanography of Coastal and Shelf Seas (ed. Johns, B. ). pp. 189–266. Elsevier.Google Scholar
38. Spalart, P. R., Jou, W. H., Strelets, M. & Allmaras, S. R. 1997 Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. In Proceedings of the 1st AFOSR International Conference on DNS/LES, 4–8 August 1997 (ed. Liu, C. & Liu, Z. ). Advances in DNS/LES, pp. 137–147. Greyden.Google Scholar
39. Tafti, D. K. & Vanka, S. P. 1991 A numerical study of the effects of spanwise rotation on turbulent channel flow. Phys. Fluids 3, 642.Google Scholar
40. Taylor, J. R., Sarkar, S. & Armenio, V. 2005 Large eddy simulation of stably stratified open channel flow. Phys. Fluids 17, 116602.CrossRefGoogle Scholar
41. Tritton, D. J. 1978 Turbulence in rotating fluids. In Rotating Fluids in Geophysics (ed. Roberts, P. H. & Soward, A. M. ). pp. 105–138. Academic.Google Scholar
42. Tritton, D. J. 1992 Stabilization and destabilization of turbulent shear flow in a rotating fluid. J. Fluid Mech. 241, 503–523.Google Scholar
43. Weatherly, G. L. 1975 A numerical study of time-dependent turbulent Ekman layers over horizontal and sloping bottoms. J. Phys. Oceanogr. 5, 288–299.Google Scholar
44. Weatherly, G. L., Blumsack, S. L. & Bird, A. A. 1980 On the effect of diurnal tidal currents in determining the thickness of the turbulent Ekman bottom boundary layer. J. Phys. Oceanogr. 10, 297–300.Google Scholar
45. Wu, H. & Kasagi, N. 2004 Effects of arbitrary directional system rotation on turbulent channel flow. Phys. Fluids 16, 979–990.CrossRefGoogle Scholar
46. Zang, Y. & Street, L. R. 1995 Numerical simulation of coastal upwelling and interfacial instability of a rotating and stratified fluid. J. Fluid Mech. 305, 47–75.Google Scholar
47. Zang, Y., Street, R. L. & Koseff, J. R. 1994 A non-staggered grid, fractional step method for time-dependent incompressible Navier–Stokes equations in curvilinear co-ordinates. J. Comput. Phys. 114, 18.Google Scholar
48. Zikanov, O., Slinn, D. N. & Dhanak, M. R. 2003 Large-eddy simulations of the wind-induced turbulent Ekman layer. J. Fluid Mech. 495, 343–368.Google Scholar