Article contents
A numerical study of shear layer characteristics of low-speed transverse jets
Published online by Cambridge University Press: 03 February 2016
Abstract
Direct numerical simulation (DNS) and dynamic mode decomposition (DMD) are used to study the shear layer characteristics of a jet in a crossflow. Experimental observations by Megerian et al. (J. Fluid Mech., vol. 593, 2007, pp. 93–129) at velocity ratios ( 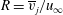 $R=\overline{v}_{j}/u_{\infty }$ ) of 2 and 4 and Reynolds number (
$R=\overline{v}_{j}/u_{\infty }$ ) of 2 and 4 and Reynolds number ( 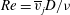 $Re=\overline{v}_{j}D/{\it\nu}$ ) of 2000 on the transition from absolute to convective instability of the upstream shear layer are reproduced. Point velocity spectra at different points along the shear layer show excellent agreement with experiments. The same frequency (
$Re=\overline{v}_{j}D/{\it\nu}$ ) of 2000 on the transition from absolute to convective instability of the upstream shear layer are reproduced. Point velocity spectra at different points along the shear layer show excellent agreement with experiments. The same frequency ( 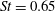 $St=0.65$ ) is dominant along the length of the shear layer for
$St=0.65$ ) is dominant along the length of the shear layer for 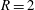 $R=2$ , whereas the dominant frequencies change along the shear layer for
$R=2$ , whereas the dominant frequencies change along the shear layer for 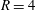 $R=4$ . DMD of the full three-dimensional flow field is able to reproduce the dominant frequencies observed from DNS and shows that the shear layer modes are dominant for both the conditions simulated. The spatial modes obtained from DMD are used to study the nature of the shear layer instability. It is found that a counter-current mixing layer is obtained in the upstream shear layer. The corresponding mixing velocity ratio is obtained, and seen to delineate the two regimes of absolute or convective instability. The effect of the nozzle is evaluated by performing simulations without the nozzle while requiring the jet to have the same inlet velocity profile as that obtained at the nozzle exit in the simulations including the nozzle. The shear layer spectra show good agreement with the simulations including the nozzle. The effect of shear layer thickness is studied at a velocity ratio of 2 based on peak and mean jet velocity. The dominant frequencies and spatial shear layer modes from DNS/DMD are significantly altered by the jet exit velocity profile.
$R=4$ . DMD of the full three-dimensional flow field is able to reproduce the dominant frequencies observed from DNS and shows that the shear layer modes are dominant for both the conditions simulated. The spatial modes obtained from DMD are used to study the nature of the shear layer instability. It is found that a counter-current mixing layer is obtained in the upstream shear layer. The corresponding mixing velocity ratio is obtained, and seen to delineate the two regimes of absolute or convective instability. The effect of the nozzle is evaluated by performing simulations without the nozzle while requiring the jet to have the same inlet velocity profile as that obtained at the nozzle exit in the simulations including the nozzle. The shear layer spectra show good agreement with the simulations including the nozzle. The effect of shear layer thickness is studied at a velocity ratio of 2 based on peak and mean jet velocity. The dominant frequencies and spatial shear layer modes from DNS/DMD are significantly altered by the jet exit velocity profile.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 64
- Cited by


