Article contents
Numerical study of viscoelastic upstream instability
Published online by Cambridge University Press: 17 March 2023
Abstract
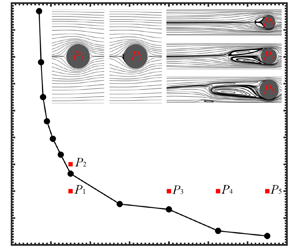
In this work, we report numerical results on the flow instability and bifurcation of a viscoelastic fluid in the upstream region of a cylinder in a confined narrow channel. Two-dimensional direct numerical simulations based on the FENE-P model (the finite-extensible nonlinear elastic model with the Peterlin closure) are conducted with numerical stabilization techniques. Our results show that the macroscopic viscoelastic constitutive relation can capture the viscoelastic upstream instability reported in previous experiments for low-Reynolds-number flows. The numerical simulations reveal that the non-dimensional recirculation length (LD) is affected by the cylinder blockage ratio (BR), the Weissenberg number (Wi), the viscosity ratio (β) and the maximum polymer extension (L). Close to the onset of upstream recirculation, LD with Wi satisfy Landau-type quartic potential under certain parameter space. The bifurcation may exhibit subcritical behaviour depending on the values of L2 and β. The parameters β and L2 have nonlinear influence on the upstream recirculation length. This work contributes to our theoretical understanding of this new instability mechanism in viscoelastic wake flows.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 7
- Cited by


