Article contents
On coherent structure in wall turbulence
Published online by Cambridge University Press: 08 July 2013
Abstract
A new theory of coherent structure in wall turbulence is presented. The theory is the first to predict packets of hairpin vortices and other structure in turbulence, and their dynamics, based on an analysis of the Navier–Stokes equations, under an assumption of a turbulent mean profile. The assumption of the turbulent mean acts as a restriction on the class of possible structures. It is shown that the coherent structure is a manifestation of essentially low-dimensional flow dynamics, arising from a critical-layer mechanism. Using the decomposition presented in McKeon & Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382), complex coherent structure is recreated from minimal superpositions of response modes predicted by the analysis, which take the form of radially varying travelling waves. The leading modes effectively constitute a low-dimensional description of the turbulent flow, which is optimal in the sense of describing the resonant effects around the critical layer and which minimally predicts all types of structure. The approach is general for the full range of scales. By way of example, simple combinations of these modes are offered that predict hairpins and modulated hairpin packets. The example combinations are chosen to represent observed structure, consistent with the nonlinear triadic interaction for wavenumbers that is required for self-interaction of structures. The combination of the three leading response modes at streamwise wavenumbers  $6, ~1, ~7$ and spanwise wavenumbers
$6, ~1, ~7$ and spanwise wavenumbers 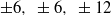 $\pm 6, ~\pm 6, ~\pm 12$ , respectively, with phase velocity
$\pm 6, ~\pm 6, ~\pm 12$ , respectively, with phase velocity 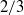 $2/ 3$ , is understood to represent a turbulence ‘kernel’, which, it is proposed, constitutes a self-exciting process analogous to the near-wall cycle. Together, these interactions explain how the mode combinations may self-organize and self-sustain to produce experimentally observed structure. The phase interaction also leads to insight into skewness and correlation results known in the literature. It is also shown that the very large-scale motions act to organize hairpin-like structures such that they co-locate with areas of low streamwise momentum, by a mechanism of locally altering the shear profile. These energetic streamwise structures arise naturally from the resolvent analysis, rather than by a summation of hairpin packets. In addition, these packets are modulated through a ‘beat’ effect. The relationship between Taylor’s hypothesis and coherence is discussed, and both are shown to be the consequence of the localization of the response modes around the critical layer. A pleasing link is made to the classical laminar inviscid theory, whereby the essential mechanism underlying the hairpin vortex is captured by two obliquely interacting Kelvin–Stuart (cat’s eye) vortices. Evidence for the theory is presented based on comparison with observations of structure in turbulent flow reported in the experimental and numerical simulation literature and with exact solutions reported in the transitional literature.
$2/ 3$ , is understood to represent a turbulence ‘kernel’, which, it is proposed, constitutes a self-exciting process analogous to the near-wall cycle. Together, these interactions explain how the mode combinations may self-organize and self-sustain to produce experimentally observed structure. The phase interaction also leads to insight into skewness and correlation results known in the literature. It is also shown that the very large-scale motions act to organize hairpin-like structures such that they co-locate with areas of low streamwise momentum, by a mechanism of locally altering the shear profile. These energetic streamwise structures arise naturally from the resolvent analysis, rather than by a summation of hairpin packets. In addition, these packets are modulated through a ‘beat’ effect. The relationship between Taylor’s hypothesis and coherence is discussed, and both are shown to be the consequence of the localization of the response modes around the critical layer. A pleasing link is made to the classical laminar inviscid theory, whereby the essential mechanism underlying the hairpin vortex is captured by two obliquely interacting Kelvin–Stuart (cat’s eye) vortices. Evidence for the theory is presented based on comparison with observations of structure in turbulent flow reported in the experimental and numerical simulation literature and with exact solutions reported in the transitional literature.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 166
- Cited by

