Article contents
On quasi-steady boundary-layer separation in supersonic flow. Part 2. Downstream moving separation point
Published online by Cambridge University Press: 03 August 2020
Abstract
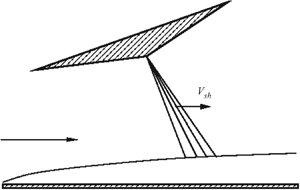
In this paper we study the perturbations produced in the boundary layer by an impinging oblique shock wave or Prandtl–Meyer expansion fan. The flow outside the boundary layer is assumed supersonic, and we also assume that the point, where the shock wave/expansion fan impinges on the boundary layer, moves downstream. To study the flow, it is convenient to use the coordinate frame moving with the shock; in this frame, the body surface moves upstream. We first study numerically the case when the shock velocity  $V_{sh} = O (Re^{-1/8})$. In this case the interaction of the boundary layer with the shock can be described by the classical equations of the triple-deck theory. We find that, as
$V_{sh} = O (Re^{-1/8})$. In this case the interaction of the boundary layer with the shock can be described by the classical equations of the triple-deck theory. We find that, as  $V_{sh}$ increases, the boundary layer proves to be more prone to separation when exposed to the expansion fan, not the compression shock. Then we assume
$V_{sh}$ increases, the boundary layer proves to be more prone to separation when exposed to the expansion fan, not the compression shock. Then we assume  $V_{sh}$ to be in the range
$V_{sh}$ to be in the range  $1 \gg V_{sh} \gg Re^{-1/8}$. Under these conditions, the process of the interaction between the boundary layer and the shock/expansion fan can be treated as inviscid and quasi-steady if considered in the reference frame moving with the shock/expansion fan. The inviscid analysis allows us to determine the pressure distribution in the interaction region. We then turn our attention to a thin viscous sublayer that lies closer to the body surface. In this sublayer the flow is described by classical Prandtl's equations. The solution to these equations develops a singularity provided that the expansion fan is strong enough. The flow analysis in a small vicinity of the singular point shows an accelerated ‘expansion’ of the flow similar to the one reported by Neiland (Izv. Akad. Nauk SSSR, Mech. Zhidk. Gaza, vol. 5, 1969a, pp. 53–60) in his analysis of supersonic flow separation from a convex corner.
$1 \gg V_{sh} \gg Re^{-1/8}$. Under these conditions, the process of the interaction between the boundary layer and the shock/expansion fan can be treated as inviscid and quasi-steady if considered in the reference frame moving with the shock/expansion fan. The inviscid analysis allows us to determine the pressure distribution in the interaction region. We then turn our attention to a thin viscous sublayer that lies closer to the body surface. In this sublayer the flow is described by classical Prandtl's equations. The solution to these equations develops a singularity provided that the expansion fan is strong enough. The flow analysis in a small vicinity of the singular point shows an accelerated ‘expansion’ of the flow similar to the one reported by Neiland (Izv. Akad. Nauk SSSR, Mech. Zhidk. Gaza, vol. 5, 1969a, pp. 53–60) in his analysis of supersonic flow separation from a convex corner.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by

