Article contents
On the formation of axial corner vortices during spin-up in a cylinder of square cross-section
Published online by Cambridge University Press: 05 May 2015
Abstract
We present experimental and theoretical results for the adjustment of a fluid (homogeneous or linearly stratified), which is initially rotating as a solid body with angular frequency 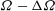 ${\it\Omega}-{\rm\Delta}{\it\Omega}$ , to a nonlinear increase
${\it\Omega}-{\rm\Delta}{\it\Omega}$ , to a nonlinear increase 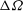 ${\rm\Delta}{\it\Omega}$ in the angular frequency of all bounding surfaces. The fluid is contained in a cylinder of square cross-section which is aligned centrally along the rotation axis, and we focus on the
${\rm\Delta}{\it\Omega}$ in the angular frequency of all bounding surfaces. The fluid is contained in a cylinder of square cross-section which is aligned centrally along the rotation axis, and we focus on the 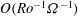 $O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$ time scale, where
$O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$ time scale, where 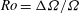 $\mathit{Ro}={\rm\Delta}{\it\Omega}/{\it\Omega}$ is the Rossby number. The flow development is shown to be dominated by unsteady separation of a viscous sidewall layer, leading to an eruption of vorticity that becomes trapped in the four vertical corners of the container. The longer-time evolution on the standard ‘spin-up’ time scale,
$\mathit{Ro}={\rm\Delta}{\it\Omega}/{\it\Omega}$ is the Rossby number. The flow development is shown to be dominated by unsteady separation of a viscous sidewall layer, leading to an eruption of vorticity that becomes trapped in the four vertical corners of the container. The longer-time evolution on the standard ‘spin-up’ time scale, 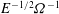 $E^{-1/2}{\it\Omega}^{-1}$ (where
$E^{-1/2}{\it\Omega}^{-1}$ (where 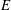 $E$ is the associated Ekman number), has been described in detail for this geometry by Foster & Munro (J. Fluid Mech., vol. 712, 2012, pp. 7–40), but only for small changes in the container’s rotation rate (i.e.
$E$ is the associated Ekman number), has been described in detail for this geometry by Foster & Munro (J. Fluid Mech., vol. 712, 2012, pp. 7–40), but only for small changes in the container’s rotation rate (i.e. 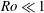 $\mathit{Ro}\ll 1$ ). In the linear case, for
$\mathit{Ro}\ll 1$ ). In the linear case, for 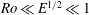 $\mathit{Ro}\ll E^{1/2}\ll 1$ , there is no sidewall separation. In the present investigation we focus on the fully nonlinear problem,
$\mathit{Ro}\ll E^{1/2}\ll 1$ , there is no sidewall separation. In the present investigation we focus on the fully nonlinear problem, 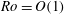 $\mathit{Ro}=O(1)$ , for which the sidewall viscous layers are Prandtl boundary layers and (somewhat unusually) periodic around the container’s circumference. Some care is required in the corners of the container, but we show that the sidewall boundary layer breaks down (separates) shortly after an impulsive change in rotation rate. These theoretical boundary-layer results are compared with two-dimensional Navier–Stokes results which capture the eruption of vorticity, and these are in turn compared to laboratory observations and data. The experiments show that when the Burger number,
$\mathit{Ro}=O(1)$ , for which the sidewall viscous layers are Prandtl boundary layers and (somewhat unusually) periodic around the container’s circumference. Some care is required in the corners of the container, but we show that the sidewall boundary layer breaks down (separates) shortly after an impulsive change in rotation rate. These theoretical boundary-layer results are compared with two-dimensional Navier–Stokes results which capture the eruption of vorticity, and these are in turn compared to laboratory observations and data. The experiments show that when the Burger number, 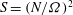 $S=(N/{\it\Omega})^{2}$ (where
$S=(N/{\it\Omega})^{2}$ (where 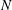 $N$ is the buoyancy frequency), is relatively large – corresponding to a strongly stratified fluid – the flow remains (horizontally) two-dimensional on the
$N$ is the buoyancy frequency), is relatively large – corresponding to a strongly stratified fluid – the flow remains (horizontally) two-dimensional on the 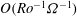 $O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$ time scale, and good quantitative predictions can be made by a two-dimensional theory. As
$O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$ time scale, and good quantitative predictions can be made by a two-dimensional theory. As 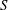 $S$ was reduced in the experiments, three-dimensional effects were observed to become important in the core of each corner vortex, on this time scale, but only after the breakdown of the sidewall layers.
$S$ was reduced in the experiments, three-dimensional effects were observed to become important in the core of each corner vortex, on this time scale, but only after the breakdown of the sidewall layers.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 5
- Cited by


