Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Peruzzi, C.
Vettori, D.
Poggi, D.
Blondeaux, P.
Ridolfi, L.
and
Manes, C.
2021.
On the influence of collinear surface waves on turbulence in smooth-bed open-channel flows.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Duan, Yanchong
Zhong, Qiang
Wang, Guiquan
Chen, Qigang
Wang, Fujun
and
Li, Danxun
2021.
Additional spanwise vortices near the free surface in open channel flows.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Iacobello, Giovanni
Ridolfi, Luca
and
Scarsoglio, Stefania
2021.
Large-to-small scale frequency modulation analysis in wall-bounded turbulence via visibility networks.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Ng, Henry C.-H.
Collignon, Emile
Poole, Robert J.
and
Dennis, David J. C.
2021.
Energetic motions in turbulent partially filled pipe flow.
Physics of Fluids,
Vol. 33,
Issue. 2,
Peruzzi, Cosimo
Galli, Andrea
Chiaradia, Enrico A.
and
Masseroni, Daniele
2021.
Evaluating longitudinal dispersion of scalars in rural channels of agro-urban environments.
Environmental Fluid Mechanics,
Vol. 21,
Issue. 4,
p.
925.
Absi, R.
2021.
Analytical Eddy Viscosity Model for Velocity Profiles in the Outer Part of Closed- and Open-Channel Flows.
Fluid Dynamics,
Vol. 56,
Issue. 4,
p.
577.
Duan, Yanchong
Zhong, Qiang
Wang, Guiquan
Zhang, Peng
and
Li, Danxun
2021.
Contributions of different scales of turbulent motions to the mean wall-shear stress in open channel flows at low-to-moderate Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Camporeale, Carlo
Cannamela, Fabio
Canuto, Claudio
and
Manes, Costantino
2021.
Stability analysis of open-channel flows with secondary currents.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Gilja, Gordon
Fliszar, Robert
Harasti, Antonija
and
Valyrakis, Manousos
2022.
Calibration and Verification of Operation Parameters for an Array of Vectrino Profilers Configured for Turbulent Flow Field Measurement around Bridge Piers—Part I.
Fluids,
Vol. 7,
Issue. 10,
p.
315.
Lama, Giuseppe Francesco Cesare
Crimaldi, Mariano
and
Chirico, Giovanni Battista
2022.
Drone-Based Ecohydraulic Signatures of Fully-Vegetated Ditches: Real-Scale Experimental Analysis.
p.
24.
Yao, Jie
Chen, Xi
and
Hussain, Fazle
2022.
Direct numerical simulation of turbulent open channel flows at moderately high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 953,
Issue. ,
Yan, Zili
Duan, Yanchong
Zhu, Dejun
and
Li, Danxun
2022.
Characteristics of very-large-scale motions in gradually varied open-channel flows upstream of a run-of-river dam.
Physics of Fluids,
Vol. 34,
Issue. 9,
Das, S.
Balachandar, R.
and
Barron, R.M.
2022.
Generation and characterization of fully developed state in open channel flow.
Journal of Fluid Mechanics,
Vol. 934,
Issue. ,
Khan, Mohammad Amir
Sharma, Nayan
Lama, Giuseppe Francesco Cesare
Hasan, Murtaza
Garg, Rishav
Busico, Gianluigi
and
Alharbi, Raied Saad
2022.
Three-Dimensional Hole Size (3DHS) Approach for Water Flow Turbulence Analysis over Emerging Sand Bars: Flume-Scale Experiments.
Water,
Vol. 14,
Issue. 12,
p.
1889.
Rastello, Marie
Klema, Matthew R.
Carpenter, Alex B.
Garanaik, Amrapalli
Venayagamoorthy, S. Karan
Gates, Timothy K.
and
Marié, J.L.
2022.
Velocity measurements in developing narrow open-channel flows with high free-stream turbulence: Acoustic Doppler Velocimetry (ADV) vs Laser Doppler Anemometry (LDA).
Flow Measurement and Instrumentation,
Vol. 87,
Issue. ,
p.
102206.
Proust, Sébastien
Berni, Céline
and
Nikora, Vladimir I.
2022.
Shallow mixing layers over hydraulically smooth bottom in a tilted open channel.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Bert, Roberto
Manes, Costantino
and
Tiraferri, Alberto
2022.
New Facility for Membrane Fouling Investigations under Customizable Hydrodynamics: Validation and Preliminary Experiments with Pulsating Cross-Flow.
Membranes,
Vol. 12,
Issue. 3,
p.
334.
Pinelli, Michele
Herlina, H.
Wissink, J.G.
and
Uhlmann, M.
2022.
Direct numerical simulation of turbulent mass transfer at the surface of an open channel flow.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Zampiron, Andrea
Cameron, Stuart M.
and
Nikora, Vladimir
2023.
On application of empirical mode decomposition for turbulence analysis in open-channel flows.
Journal of Hydraulic Research,
Vol. 61,
Issue. 5,
p.
788.
Wang, Yongqiang
Zhang, Peng
Yang, Shengfa
Hu, Chunhong
Jin, Jianling
and
Zhang, Rangang
2023.
Characteristics of Large-Scale Coherent Structures on Irregularly Arranged Rough-Bed Open-Channel Flows.
Water,
Vol. 15,
Issue. 6,
p.
1105.
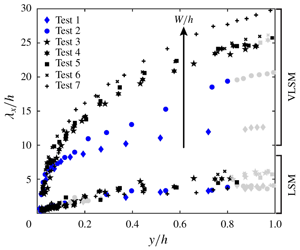
 $Re_{\unicode[STIX]{x1D70F}}$ as low as 725, whereas in other wall flows much higher values are normally required. Finally, as conjectured by a recent study on uniform rough-bed open-channel flows, the present paper confirms that LSM wavelengths scale nicely with the flow depth, whereas the channel aspect ratio (i.e. the ratio between channel width and flow depth) is the non-dimensional parameter controlling the scaling of VLSM wavelengths. The intensity and wavelengths of the VLSM peaks were also observed to depend on the spanwise coordinate. This result suggests that VLSMs might be dynamically linked to secondary currents, as these are also known to vary in strength and size across the channel width.
$Re_{\unicode[STIX]{x1D70F}}$ as low as 725, whereas in other wall flows much higher values are normally required. Finally, as conjectured by a recent study on uniform rough-bed open-channel flows, the present paper confirms that LSM wavelengths scale nicely with the flow depth, whereas the channel aspect ratio (i.e. the ratio between channel width and flow depth) is the non-dimensional parameter controlling the scaling of VLSM wavelengths. The intensity and wavelengths of the VLSM peaks were also observed to depend on the spanwise coordinate. This result suggests that VLSMs might be dynamically linked to secondary currents, as these are also known to vary in strength and size across the channel width.
