Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kidambi, Krishna Bhavithavya
Tiwari, Madhur
Jayaprakash, Anu Kossery
MacKunis, William
and
Golubev, Vladimir
2022.
A Sliding Mode Observer-based Limit Cycle Oscillation Suppression using a Robust Active Flow Control Technique.
p.
516.
Jussiau, William
Leclercq, Colin
Demourant, Fabrice
and
Apkarian, Pierre
2022.
Learning Linear Feedback Controllers for Suppressing the Vortex-Shedding Flow Past a Cylinder.
IEEE Control Systems Letters,
Vol. 6,
Issue. ,
p.
3212.
Jin, Bo
Illingworth, Simon J.
and
Sandberg, Richard D.
2022.
Resolvent-based approach for $$\pmb {H_2}$$-optimal estimation and control: an application to the cylinder flow.
Theoretical and Computational Fluid Dynamics,
Vol. 36,
Issue. 3,
p.
491.
Paris, Romain
Beneddine, Samir
and
Dandois, Julien
2023.
Reinforcement-learning-based actuator selection method for active flow control.
Journal of Fluid Mechanics,
Vol. 955,
Issue. ,
Yuan, Hao
Kou, Jiaqing
Gao, Chuanqiang
and
Zhang, Weiwei
2023.
Resolvent and dynamic mode analysis of flow past a square cylinder at subcritical Reynolds numbers.
Physics of Fluids,
Vol. 35,
Issue. 7,
Xu, Da
and
Zhang, Mengqi
2023.
Reinforcement-learning-based control of convectively unstable flows.
Journal of Fluid Mechanics,
Vol. 954,
Issue. ,
Arun, Rahul
Bae, H. Jane
and
McKeon, Beverley J.
2023.
Towards real-time reconstruction of velocity fluctuations in turbulent channel flow.
Physical Review Fluids,
Vol. 8,
Issue. 6,
Jung, Junoh
and
Towne, Aaron
2024.
Toward turbulent wake estimation using a resolvent-based approach.
Amiri-Margavi, Alireza
and
Babaee, Hessam
2024.
Time-dependent low-rank input–output operator for forced linearized dynamics with unsteady base flows.
Journal of Fluid Mechanics,
Vol. 1001,
Issue. ,
Déda, Tarcísio C.
Wolf, William R.
and
Dawson, Scott T. M.
2024.
Neural networks in feedback for flow analysis and control.
Physical Review Fluids,
Vol. 9,
Issue. 6,
Xu, Zhaoyue
Wang, Shizhao
Zhang, Xin-Lei
and
He, Guowei
2024.
Optimal sensor placement for ensemble-based data assimilation using gradient-weighted class activation mapping.
Journal of Computational Physics,
Vol. 514,
Issue. ,
p.
113224.
Dong, Jian
Lu, Jinling
Wang, Kai
Wang, Like
and
Fu, Wei
2025.
A deep learning-based method for rapid prediction of transient loads on flexible regions of local flexible hydrofoils.
Ocean Engineering,
Vol. 342,
Issue. ,
p.
123003.
Turin, Zoe
Taylor, Graham K.
Krapp, Holger G.
Jensen, Emily
and
Sean Humbert, J.
2025.
Matching Sensing to Actuation and Dynamics in Distributed Sensorimotor Architectures.
IEEE Access,
Vol. 13,
Issue. ,
p.
13584.
Sasaki, Yasuo
Yamada, Keigo
Nagata, Takayuki
Saito, Yuji
and
Nonomura, Taku
2025.
Fast Data-Driven Greedy Sensor Selection for Ridge Regression.
IEEE Sensors Journal,
Vol. 25,
Issue. 6,
p.
10030.
Watanabe, Ayano
Takada, Naoki
Shimomura, Satoshi
Sekimoto, Satoshi
Ōtomo, Shūji
Oyama, Akira
and
Nishida, Hiroyuki
2025.
Effect of pressure sensor arrangement on deep reinforcement learning-based feedback control of separated flow around aerofoils.
Aerospace Science and Technology,
Vol. 164,
Issue. ,
p.
110347.
Ma, Rongchi
Gao, Chuanqiang
and
Zhang, Weiwei
2025.
Dependency of optimal jet control position on Reynolds-number in cylinder flow via resolvent analysis.
Physics of Fluids,
Vol. 37,
Issue. 9,
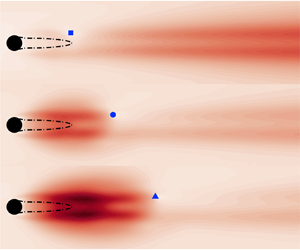
 $\mathcal {H}_2$-optimal estimators and controllers. We then investigate three control problems: (i) optimal estimation (OE) in which we measure the flow at a single location and estimate the entire flow; (ii) full-state information control (FIC) in which we measure the entire flow but actuate at only one location; and (iii) the overall feedback control problem in which a single sensor is available for measurement and a single actuator is available for control. We characterize the performance of these control arrangements over a range of sensor and actuator placements and discuss implications for effective feedback control when using a single sensor and a single actuator. The optimal sensor and actuator placements found for the OE and FIC problems are also compared with those found for the overall feedback control problem over a range of Reynolds numbers. This comparison reveals the key factors and conflicting trade-offs that limit feedback control performance.
$\mathcal {H}_2$-optimal estimators and controllers. We then investigate three control problems: (i) optimal estimation (OE) in which we measure the flow at a single location and estimate the entire flow; (ii) full-state information control (FIC) in which we measure the entire flow but actuate at only one location; and (iii) the overall feedback control problem in which a single sensor is available for measurement and a single actuator is available for control. We characterize the performance of these control arrangements over a range of sensor and actuator placements and discuss implications for effective feedback control when using a single sensor and a single actuator. The optimal sensor and actuator placements found for the OE and FIC problems are also compared with those found for the overall feedback control problem over a range of Reynolds numbers. This comparison reveals the key factors and conflicting trade-offs that limit feedback control performance.

