Article contents
A playground for compressible natural convection with a nearly uniform density
Published online by Cambridge University Press: 05 April 2022
Abstract
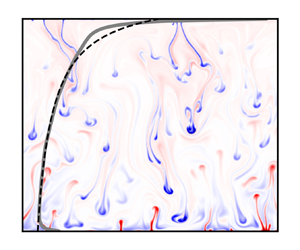
In the quest to understand the basic universal features of compressible convection, one would like to disentangle genuine consequences of compression from spatial variations of transport properties. For instance, one may choose to consider a fluid with uniform dynamic viscosity, but, then, compressible effects will generate a density gradient and consequently the kinematic viscosity will not be uniform. In the present work, we consider a very peculiar equation of state, whereby entropy is solely dependent on density, so that a nearly isentropic fluid domain is nearly isochoric. Within this class of equations of state, there is a thermal adiabatic gradient and a key property of compressible convection is still present, namely its capacity to viscously dissipate a large fraction of the thermal energy involved, of the order of the well-named dissipation number. In the anelastic approximation, under the assumption of an infinite Prandtl number, the number of governing parameters can be brought down to two, the Rayleigh number and the dissipation number. This framework is proposed as a playground for compressible convection, an opportunity to extend the vast corpus of theoretical analyses on the Oberbeck–Boussinesq equations regarding stability, bifurcations or the determination of upper bounds for the turbulent heat transfer. Here, in a two-dimensional geometry, we concentrate on the structure of numerical solutions. For all Rayleigh numbers, a change in the vertical temperature profile is observed in the range of dissipation number between  $0$ and less than
$0$ and less than  $0.4$, associated with the weakening of ascending plumes. For larger dissipation numbers, the heat flux dependence on this number is found to be well predicted by Malkus's model of critical layers. For dissipation numbers of order unity, and large Rayleigh numbers, dissipation becomes related to the entropy heat flux at each depth, so that the vertical dissipation profile can be predicted, and so does the total ratio of dissipation to convective heat flux.
$0.4$, associated with the weakening of ascending plumes. For larger dissipation numbers, the heat flux dependence on this number is found to be well predicted by Malkus's model of critical layers. For dissipation numbers of order unity, and large Rayleigh numbers, dissipation becomes related to the entropy heat flux at each depth, so that the vertical dissipation profile can be predicted, and so does the total ratio of dissipation to convective heat flux.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by


