Hostname: page-component-7bb8b95d7b-fmk2r Total loading time: 0 Render date: 2024-09-19T20:02:05.401Z Has data issue: false hasContentIssue false
  • English
  • Français

Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection

Published online by Cambridge University Press:  24 October 2011

Richard J. A. M. Stevens ,
Detlef Lohse  and
Roberto Verzicco
Richard J. A. M. Stevens*
Affiliation:
Department of Science and Technology and J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Detlef Lohse
Affiliation:
Department of Science and Technology and J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Roberto Verzicco
Affiliation:
Department of Science and Technology and J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands Department of Mechanical Engineering, Universitá di Roma ‘Tor Vergata’, Via del Politecnico 1, 00133, Roma
*
†Email address for correspondence: r.j.a.m.stevens@tnw.utwente.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

Results from direct numerical simulation for three-dimensional Rayleigh–Bénard convection in samples of aspect ratio 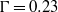and 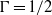up to Rayleigh number 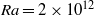are presented. The broad range of Prandtl numbers 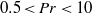is considered. In contrast to some experiments, we do not see any increase in 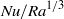with increasing 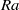, neither due to an increasing 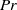, nor due to constant heat flux boundary conditions at the bottom plate instead of constant temperature boundary conditions. Even at these very high 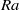, both the thermal and kinetic boundary layer thicknesses obey Prandtl–Blasius scaling.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 688 , 10 December 2011 , pp. 31 - 43
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ahlers, G., Bodenschatz, E., Funfschilling, D. & Hogg, J. 2009a Turbulent Rayleigh–Bénard convection for a Prandtl number of 0.67. J. Fluid Mech. 641, 157–167.CrossRefGoogle Scholar
2. Ahlers, G., Funfschilling, D. & Bodenschatz, E. 2009b Transitions in heat transport by turbulent convection at Rayleigh numbers up to . New J. Phys. 11, 123001.CrossRefGoogle Scholar
3. Ahlers, G., Funfschilling, D. & Bodenschatz, E. 2011 Addendum to transitions in heat transport by turbulent convection at Rayleigh numbers up to . New J. Phys. 13, 049401.CrossRefGoogle Scholar
4. Ahlers, G., Grossmann, S. & Lohse, D. 2009c Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503.CrossRefGoogle Scholar
5. Ahlers, G. & Xu, X. 2001 Prandtl-number dependence of heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 86, 3320–3323.CrossRefGoogle ScholarPubMed
6. Chavanne, X., Chilla, F., Chabaud, B., Castaing, B. & Hebral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.CrossRefGoogle Scholar
7. Chillà, F., Rastello, M., Chaumat, S. & Castaing, B. 2004 Long relaxation times and tilt sensitivity in Rayleigh–Bénard turbulence. Euro. Phys. J. B 40, 223–227.CrossRefGoogle Scholar
8. Cortet, P., Chiffaudel, A., Daviaud, F. & Dubrulle, B. 2010 Experimental evidence of a phase transition in a closed turbulent flow. Phys. Rev. Lett. 105, 214501.Google Scholar
9. Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2009 Search for the ‘ultimate state’ in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 014503.CrossRefGoogle Scholar
10. Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
11. Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle Scholar
12. Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.CrossRefGoogle ScholarPubMed
13. Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.CrossRefGoogle Scholar
14. Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
15. Hébert, F., Hufschmid, R., Scheel, J. & Ahlers, G. 2010 Onset of Rayleigh–Bénard convection in cylindrical containers. Phys. Rev. E 81, 046318.CrossRefGoogle ScholarPubMed
16. Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102, 064501.CrossRefGoogle ScholarPubMed
17. Niemela, J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
18. Niemela, J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2001 The wind in confined thermal turbulence. J. Fluid Mech. 449, 169–178.CrossRefGoogle Scholar
19. Niemela, J. & Sreenivasan, K. R. 2003 Confined turbulent convection. J. Fluid Mech. 481, 355–384.CrossRefGoogle Scholar
20. Niemela, J. & Sreenivasan, K. R. 2006 Turbulent convection at high Rayleigh numbers and aspect ratio 4. J. Fluid Mech. 557, 411–422.Google Scholar
21. Niemela, J. J. & Sreenivasan, K. R. 2010 Does confined turbulent convection ever attain the ‘asymptotic scaling’ with power? New J. Phys. 12, 115002.CrossRefGoogle Scholar
22. van der Poel, E. P., Stevens, R. J. A. M. & Lohse, D. 2011 Connecting flow structures and heat flux in turbulent Rayleigh–Bénard convection, Phys. Rev. E. (in press).CrossRefGoogle Scholar
23. Qiu, X. L. & Xia, K.-Q. 1998 Viscous boundary layers at the sidewall of a convection cell. Phys. Rev. E 58, 486–491.CrossRefGoogle Scholar
24. Roche, P. E., Castaing, B., Chabaud, B. & Hebral, B. 2001 Observation of the power law in Rayleigh–Bénard convection. Phys. Rev. E 63, 045303.CrossRefGoogle Scholar
25. Roche, P. E., Castaing, B., Chabaud, B. & Hebral, B. 2002 Prandtl and Rayleigh numbers dependences in Rayleigh–Bénard convection. Europhys. Lett. 58, 693–698.CrossRefGoogle Scholar
26. Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12, 085014.CrossRefGoogle Scholar
27. Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.CrossRefGoogle Scholar
28. Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 633, 449–460.CrossRefGoogle Scholar
29. Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010a Boundary layers in rotating weakly turbulent Rayleigh–Bénard convection. Phys. Fluids 22, 085103.CrossRefGoogle Scholar
30. Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010b Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
31. Sun, C., Cheung, Y. H. & Xia, K. Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
32. Sun, C., Xi, H.-D. & Xia, K.-Q. 2005 Azimuthal symmetry, Flow dynamics and Heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.CrossRefGoogle Scholar
33. Verzicco, R. & Camussi, R. 1997 Transitional regimes of low-prandtl thermal convection in a cylindrical cell. Phys. Fluids 9, 1287–1295.CrossRefGoogle Scholar
34. Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
35. Verzicco, R. & Sreenivasan, K. R. 2008 A comparison of turbulent thermal convection between conditions of constant temperature and constant heat flux. J. Fluid Mech. 595, 203–219.CrossRefGoogle Scholar
36. Weiss, S. & Ahlers, G. 2011 Turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ratio and Prandtl number . J. Fluid Mech. 676, 5–40.CrossRefGoogle Scholar
37. Xi, H.-D. & Xia, K.-Q. 2008 Flow mode transitions in turbulent thermal convection. Phys. Fluids 20, 055104.CrossRefGoogle Scholar
38. Xia, K.-Q., Lam, S. & Zhou, S. Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.CrossRefGoogle ScholarPubMed
39. Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
40. Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.CrossRefGoogle ScholarPubMed

Stevens et al. supplementary movies

Movie of the temperature field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.

Download Stevens et al. supplementary movies(Video)
Video 39.7 MB

Stevens et al. supplementary movies

Movie of the temperature field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.

Download Stevens et al. supplementary movies(Video)
Video 9.9 MB

Stevens et al. supplementary movies

Movie of the vertical velocity field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.

Download Stevens et al. supplementary movies(Video)
Video 40.4 MB

Stevens et al. supplementary movies

Movie of the vertical velocity field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.

Download Stevens et al. supplementary movies(Video)
Video 9.9 MB

Stevens et al. supplementary movies

Movie of the temperature field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie. This vertical cut is perpendicular to the plane shown in movie 1.

Download Stevens et al. supplementary movies(Video)
Video 34.2 MB

Stevens et al. supplementary movies

Movie of the temperature field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie. This vertical cut is perpendicular to the plane shown in movie 1.

Download Stevens et al. supplementary movies(Video)
Video 8.6 MB

Stevens et al. supplementary movies

Movie of the vertical velocity field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie. This vertical cut is perpendicular to the plane shown in movie 2.

Download Stevens et al. supplementary movies(Video)
Video 35.4 MB

Stevens et al. supplementary movies

Movie of the vertical velocity field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie. This vertical cut is perpendicular to the plane shown in movie 2.

Download Stevens et al. supplementary movies(Video)
Video 8.6 MB

Stevens et al. supplementary movies

Movie of the temperature in three horizontal planes (0:25z/L, 0:50z/L, and 0:75z/L) for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.

Download Stevens et al. supplementary movies(Video)
Video 50.7 MB

Stevens et al. supplementary movies

Movie of the temperature in three horizontal planes (0:25z/L, 0:50z/L, and 0:75z/L) for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.

Download Stevens et al. supplementary movies(Video)
Video 9.9 MB

Stevens et al. supplementary movies

Movie of the vertical velocity field in three horizontal planes (0:25z/L, 0:50z/L, and 0:75z/L) for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.

Download Stevens et al. supplementary movies(Video)
Video 52.3 MB

Stevens et al. supplementary movies

Movie of the vertical velocity field in three horizontal planes (0:25z/L, 0:50z/L, and 0:75z/L) for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.

Download Stevens et al. supplementary movies(Video)
Video 9.9 MB