Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hearst, R. J.
and
Ganapathisubramani, B.
2015.
Quantification and adjustment of pixel-locking in particle image velocimetry.
Experiments in Fluids,
Vol. 56,
Issue. 10,
Chan, L.
MacDonald, M.
Chung, D.
Hutchins, N.
and
Ooi, A.
2015.
A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime.
Journal of Fluid Mechanics,
Vol. 771,
Issue. ,
p.
743.
Rochlitz, Henrik
Scholz, Peter
and
Fuchs, Thomas
2015.
The flow field in a high aspect ratio cooling duct with and without one heated wall.
Experiments in Fluids,
Vol. 56,
Issue. 12,
Yang, Jongmin
Hwang, Jinyul
and
Sung, Hyung Jin
2016.
Structural organization of the quiescent core region in a turbulent channel flow.
International Journal of Heat and Fluid Flow,
Vol. 62,
Issue. ,
p.
455.
de Silva, Charitha M.
Hutchins, Nicholas
and
Marusic, Ivan
2016.
Uniform momentum zones in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 786,
Issue. ,
p.
309.
Vanderwel, Christina
and
Tavoularis, Stavros
2016.
Scalar dispersion by coherent structures in uniformly sheared flow generated in a water tunnel.
Journal of Turbulence,
Vol. 17,
Issue. 7,
p.
633.
Krug, Dominik
Philip, Jimmy
and
Marusic, Ivan
2017.
Revisiting the law of the wake in wall turbulence.
Journal of Fluid Mechanics,
Vol. 811,
Issue. ,
p.
421.
de Silva, Charitha M.
Philip, Jimmy
Hutchins, Nicholas
and
Marusic, Ivan
2017.
Interfaces of uniform momentum zones in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
451.
Elsnab, John R.
Monty, Jason P.
White, Christopher M.
Koochesfahani, Manoochehr M.
and
Klewicki, Joseph C.
2017.
Efficacy of single-component MTV to measure turbulent wall-flow velocity derivative profiles at high resolution.
Experiments in Fluids,
Vol. 58,
Issue. 9,
Stella, Francesco
Mazellier, Nicolas
and
Kourta, Azeddine
2017.
Scaling of separated shear layers: an investigation of mass entrainment.
Journal of Fluid Mechanics,
Vol. 826,
Issue. ,
p.
851.
Lee, Jin
Sung, Hyung Jin
and
Zaki, Tamer A.
2017.
Signature of large-scale motions on turbulent/non-turbulent interface in boundary layers.
Journal of Fluid Mechanics,
Vol. 819,
Issue. ,
p.
165.
Gruber, Andrea
Richardson, Edward S.
Aditya, Konduri
and
Chen, Jacqueline H.
2018.
Direct numerical simulations of premixed and stratified flame propagation in turbulent channel flow.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Laskari, A.
de Kat, R.
Hearst, R. J.
and
Ganapathisubramani, B.
2018.
Time evolution of uniform momentum zones in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 842,
Issue. ,
p.
554.
Xu, Haosen H. A.
and
Yang, X. I. A.
2018.
Fractality and the law of the wall.
Physical Review E,
Vol. 97,
Issue. 5,
Hwang, Jinyul
and
Sung, Hyung Jin
2018.
Wall-attached structures of velocity fluctuations in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 856,
Issue. ,
p.
958.
Heisel, Michael
Dasari, Teja
Liu, Yun
Hong, Jiarong
Coletti, Filippo
and
Guala, Michele
2018.
The spatial structure of the logarithmic region in very-high-Reynolds-number rough wall turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 857,
Issue. ,
p.
704.
Yang, Jongmin
Hwang, Jinyul
and
Sung, Hyung Jin
2019.
Influence of wall-attached structures on the boundary of the quiescent core region in turbulent pipe flow.
Physical Review Fluids,
Vol. 4,
Issue. 11,
Bautista, Juan Carlos Cuevas
Ebadi, Alireza
White, Christopher M.
Chini, Gregory P.
and
Klewicki, Joseph C.
2019.
A uniform momentum zone–vortical fissure model of the turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 858,
Issue. ,
p.
609.
Elsinga, G. E.
and
da Silva, C. B.
2019.
How the turbulent/non-turbulent interface is different from internal turbulence.
Journal of Fluid Mechanics,
Vol. 866,
Issue. ,
p.
216.
Fan, Duosi
Xu, Jinglei
Yao, Matthew X.
and
Hickey, Jean-Pierre
2019.
On the detection of internal interfacial layers in turbulent flows.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
198.
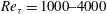 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Re_{\tau } = 1000\text {--}4000$ , it was found that the ‘core’ is identifiable by regions bounded by the continuous isocontour lines of the streamwise velocity at
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Re_{\tau } = 1000\text {--}4000$ , it was found that the ‘core’ is identifiable by regions bounded by the continuous isocontour lines of the streamwise velocity at 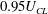 $0.95U_{CL}$ (95 % of the centreline velocity). A detailed investigation into the properties of the core has revealed it has a large-scale oscillation which is predominantly anti-symmetric with respect to the channel centreline as it moves through the channel, and there is a distinct jump in turbulence statistics as the core boundary is crossed. It is concluded that the edge of the core demarcates a shear layer of relatively intense vorticity such that the interior of the core contains weakly varying, very low-level turbulence (relative to the flow closer to the wall). Although channel flows are generally referred to as ‘fully turbulent’, these findings suggest there exists a relatively large and ‘quiescent’ core region with a boundary qualitatively similar to the turbulent/non-turbulent interface of boundary layers, jets and wakes.
$0.95U_{CL}$ (95 % of the centreline velocity). A detailed investigation into the properties of the core has revealed it has a large-scale oscillation which is predominantly anti-symmetric with respect to the channel centreline as it moves through the channel, and there is a distinct jump in turbulence statistics as the core boundary is crossed. It is concluded that the edge of the core demarcates a shear layer of relatively intense vorticity such that the interior of the core contains weakly varying, very low-level turbulence (relative to the flow closer to the wall). Although channel flows are generally referred to as ‘fully turbulent’, these findings suggest there exists a relatively large and ‘quiescent’ core region with a boundary qualitatively similar to the turbulent/non-turbulent interface of boundary layers, jets and wakes.