Article contents
Receptivity of the boundary layer to vibrations of the wing surface
Published online by Cambridge University Press: 16 April 2013
Abstract
In this paper we study the generation of Tollmien–Schlichting waves in the boundary layer due to elastic vibrations of the wing surface. The subsonic flow regime is considered with the Mach number outside the boundary layer 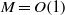 $M= O(1)$ . The flow is investigated based on the asymptotic analysis of the Navier–Stokes equations at large values of the Reynolds number,
$M= O(1)$ . The flow is investigated based on the asymptotic analysis of the Navier–Stokes equations at large values of the Reynolds number, 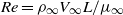 $\mathit{Re}= {\rho }_{\infty } {V}_{\infty } L/ {\mu }_{\infty } $ . Here
$\mathit{Re}= {\rho }_{\infty } {V}_{\infty } L/ {\mu }_{\infty } $ . Here 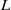 $L$ denotes the wing section chord; and
$L$ denotes the wing section chord; and 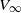 ${V}_{\infty } $ ,
${V}_{\infty } $ , 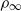 ${\rho }_{\infty } $ and
${\rho }_{\infty } $ and 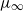 ${\mu }_{\infty } $ are the free stream velocity, air density and dynamic viscosity, respectively. We assume that in the spectrum of the wing vibrations there is a harmonic that comes in to resonance with the Tollmien–Schlichting wave on the lower branch of the stability curve; this happens when the frequency of the harmonic is a quantity of the order of
${\mu }_{\infty } $ are the free stream velocity, air density and dynamic viscosity, respectively. We assume that in the spectrum of the wing vibrations there is a harmonic that comes in to resonance with the Tollmien–Schlichting wave on the lower branch of the stability curve; this happens when the frequency of the harmonic is a quantity of the order of 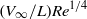 $({V}_{\infty } / L){\mathit{Re}}^{1/ 4} $ . The wavelength,
$({V}_{\infty } / L){\mathit{Re}}^{1/ 4} $ . The wavelength, 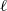 $\ell $ , of the elastic vibrations of the wing is assumed to be
$\ell $ , of the elastic vibrations of the wing is assumed to be 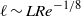 $\ell \sim L{\mathit{Re}}^{- 1/ 8} $ , which has been found to represent a ‘distinguished limit’ in the theory. Still, the results of the analysis are applicable for
$\ell \sim L{\mathit{Re}}^{- 1/ 8} $ , which has been found to represent a ‘distinguished limit’ in the theory. Still, the results of the analysis are applicable for 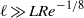 $\ell \gg L{\mathit{Re}}^{- 1/ 8} $ and
$\ell \gg L{\mathit{Re}}^{- 1/ 8} $ and 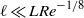 $\ell \ll L{\mathit{Re}}^{- 1/ 8} $ ; the former includes an important case when
$\ell \ll L{\mathit{Re}}^{- 1/ 8} $ ; the former includes an important case when 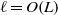 $\ell = O(L)$ . We found that the vibrations of the wing surface produce pressure perturbations in the flow outside the boundary layer, which can be calculated with the help of the ‘piston theory’, which remains valid provided that the Mach number,
$\ell = O(L)$ . We found that the vibrations of the wing surface produce pressure perturbations in the flow outside the boundary layer, which can be calculated with the help of the ‘piston theory’, which remains valid provided that the Mach number, 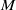 $M$ , is large as compared to
$M$ , is large as compared to 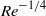 ${\mathit{Re}}^{- 1/ 4} $ . As the pressure perturbations penetrate into the boundary layer, a Stokes layer forms on the wing surface; its thickness is estimated as a quantity of the order of
${\mathit{Re}}^{- 1/ 4} $ . As the pressure perturbations penetrate into the boundary layer, a Stokes layer forms on the wing surface; its thickness is estimated as a quantity of the order of 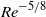 ${\mathit{Re}}^{- 5/ 8} $ . When
${\mathit{Re}}^{- 5/ 8} $ . When 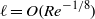 $\ell = O({\mathit{Re}}^{- 1/ 8} )$ or
$\ell = O({\mathit{Re}}^{- 1/ 8} )$ or 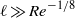 $\ell \gg {\mathit{Re}}^{- 1/ 8} $ , the solution in the Stokes layer appears to be influenced significantly by the compressibility of the flow. The Stokes layer on its own is incapable of producing the Tollmien–Schlichting waves. The reason is that the characteristic wavelength of the perturbation field in the Stokes layer is much larger than that of the Tollmien–Schlichting wave. However, the situation changes when the Stokes layer encounters a wall roughness, which are plentiful in real aerodynamic flows. If the longitudinal extent of the roughness is a quantity of the order of
$\ell \gg {\mathit{Re}}^{- 1/ 8} $ , the solution in the Stokes layer appears to be influenced significantly by the compressibility of the flow. The Stokes layer on its own is incapable of producing the Tollmien–Schlichting waves. The reason is that the characteristic wavelength of the perturbation field in the Stokes layer is much larger than that of the Tollmien–Schlichting wave. However, the situation changes when the Stokes layer encounters a wall roughness, which are plentiful in real aerodynamic flows. If the longitudinal extent of the roughness is a quantity of the order of 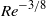 ${\mathit{Re}}^{- 3/ 8} $ , then efficient generation of the Tollmien–Schlichting waves becomes possible. In this paper we restrict our attention to the case when the Stokes layer interacts with an isolated roughness. The flow near the roughness is described by the triple-deck theory. The solution of the triple-deck problem can be found in an analytic form. Our main concern is with the flow behaviour downstream of the roughness and, in particular, with the amplitude of the generated Tollmien–Schlichting waves.
${\mathit{Re}}^{- 3/ 8} $ , then efficient generation of the Tollmien–Schlichting waves becomes possible. In this paper we restrict our attention to the case when the Stokes layer interacts with an isolated roughness. The flow near the roughness is described by the triple-deck theory. The solution of the triple-deck problem can be found in an analytic form. Our main concern is with the flow behaviour downstream of the roughness and, in particular, with the amplitude of the generated Tollmien–Schlichting waves.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 22
- Cited by

