Published online by Cambridge University Press: 18 November 2022
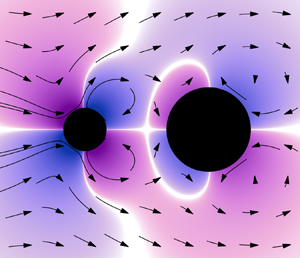
In Stokes flow, Purcell's scallop theorem forbids objects with time-reversible (reciprocal) swimming strokes from moving. In the presence of inertia, this restriction is eased and reciprocally deforming bodies can swim. A number of recent works have investigated dimer models that swim reciprocally at intermediate Reynolds numbers  ${\textit Re} \approx 1$–1000. These show interesting results (e.g. switches of the swim direction as a function of inertia) but the results vary and seem to be case specific. Here, we introduce a general model and investigate the behaviour of an asymmetric spherical dimer of oscillating length for small-amplitude motion at intermediate
${\textit Re} \approx 1$–1000. These show interesting results (e.g. switches of the swim direction as a function of inertia) but the results vary and seem to be case specific. Here, we introduce a general model and investigate the behaviour of an asymmetric spherical dimer of oscillating length for small-amplitude motion at intermediate  ${\textit {Re}}$. In our analysis we make the important distinction between particle and fluid inertia, both of which need to be considered separately. We asymptotically expand the Navier–Stokes equations in the small-amplitude limit to obtain a system of linear partial differential equations. Using a combination of numerical (finite element) and analytical (reciprocal theorem, method of reflections) methods we solve the system to obtain the dimer's swim speed and show that there are two mechanisms that give rise to motion: boundary conditions (an effective slip velocity) and Reynolds stresses. Each mechanism is driven by two classes of sphere–sphere interactions, between one sphere's motion and (1) the oscillating background flow induced by the other's motion, and (2) a geometric asymmetry induced by the other's presence. We can thus unify and explain behaviours observed in other works. Our results show how sensitive, counterintuitive and rich motility is in the parameter space of finite inertia of particles and fluid.
${\textit {Re}}$. In our analysis we make the important distinction between particle and fluid inertia, both of which need to be considered separately. We asymptotically expand the Navier–Stokes equations in the small-amplitude limit to obtain a system of linear partial differential equations. Using a combination of numerical (finite element) and analytical (reciprocal theorem, method of reflections) methods we solve the system to obtain the dimer's swim speed and show that there are two mechanisms that give rise to motion: boundary conditions (an effective slip velocity) and Reynolds stresses. Each mechanism is driven by two classes of sphere–sphere interactions, between one sphere's motion and (1) the oscillating background flow induced by the other's motion, and (2) a geometric asymmetry induced by the other's presence. We can thus unify and explain behaviours observed in other works. Our results show how sensitive, counterintuitive and rich motility is in the parameter space of finite inertia of particles and fluid.