Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Paul, I.
Papadakis, G.
and
Vassilicos, J. C.
2018.
Direct numerical simulation of heat transfer from a cylinder immersed in the production and decay regions of grid-element turbulence.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
452.
Zhou, Yi
Nagata, Koji
Sakai, Yasuhiko
and
Watanabe, Tomoaki
2018.
Dual-plane turbulent jets and their non-Gaussian velocity fluctuations.
Physical Review Fluids,
Vol. 3,
Issue. 12,
Silva, Tiago S.
Zecchetto, Marco
and
da Silva, Carlos B.
2018.
The scaling of the turbulent/non-turbulent interface at high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 843,
Issue. ,
p.
156.
Breda, M.
and
Buxton, O. R. H.
2019.
Behaviour of small-scale turbulence in the turbulent/non-turbulent interface region of developing turbulent jets.
Journal of Fluid Mechanics,
Vol. 879,
Issue. ,
p.
187.
Wu, Zhao
Lee, Jin
Meneveau, Charles
and
Zaki, Tamer
2019.
Application of a self-organizing map to identify the turbulent-boundary-layer interface in a transitional flow.
Physical Review Fluids,
Vol. 4,
Issue. 2,
Tao, Shancong
and
Zhou, Yi
2019.
Turbulent flows around side-by-side cylinders with regular and multiscale arrangements.
Physical Review Fluids,
Vol. 4,
Issue. 12,
Wu, Di
Wang, Jinjun
and
Pan, Chong
2020.
Bubbles and drops in the vicinity of turbulent/non-turbulent interface in turbulent boundary layers.
Experiments in Fluids,
Vol. 61,
Issue. 11,
Xiao, Heng
Wu, Jin-Long
Laizet, Sylvain
and
Duan, Lian
2020.
Flows over periodic hills of parameterized geometries: A dataset for data-driven turbulence modeling from direct simulations.
Computers & Fluids,
Vol. 200,
Issue. ,
p.
104431.
Kankanwadi, Krishna S.
and
Buxton, Oliver R. H.
2020.
Turbulent entrainment into a cylinder wake from a turbulent background.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Bartholomew, Paul
Deskos, Georgios
Frantz, Ricardo A.S.
Schuch, Felipe N.
Lamballais, Eric
and
Laizet, Sylvain
2020.
Xcompact3D: An open-source framework for solving turbulence problems on a Cartesian mesh.
SoftwareX,
Vol. 12,
Issue. ,
p.
100550.
Cafiero, Gioacchino
and
Vassilicos, J. Christos
2020.
Non-equilibrium Scaling of the Turbulent-Nonturbulent Interface Speed in Planar Jets.
Physical Review Letters,
Vol. 125,
Issue. 17,
Zhou, Y.
and
Vassilicos, J. C.
2020.
Energy cascade at the turbulent/nonturbulent interface.
Physical Review Fluids,
Vol. 5,
Issue. 6,
Zhou, Yi
Nagata, Koji
Sakai, Yasuhiko
Watanabe, Tomoaki
Ito, Yasumasa
and
Hayase, Toshiyuki
2020.
Energy transfer in turbulent flows behind two side-by-side square cylinders.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Wu, Di
Wang, JinJun
Cui, GuangYao
and
Pan, Chong
2020.
Effects of surface shapes on properties of turbulent/non-turbulent interface in turbulent boundary layers.
Science China Technological Sciences,
Vol. 63,
Issue. 2,
p.
214.
Hayashi, Masato
Watanabe, Tomoaki
and
Nagata, Koji
2021.
Characteristics of small-scale shear layers in a temporally evolving turbulent planar jet.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Zhao, H. K.
Liu, Y. W.
Shao, L.
Fang, L.
and
Dong, M.
2021.
Existence of positive skewness of velocity gradient in early transition.
Physical Review Fluids,
Vol. 6,
Issue. 10,
van Reeuwijk, Maarten
Vassilicos, J. Christos
and
Craske, John
2021.
Unified description of turbulent entrainment.
Journal of Fluid Mechanics,
Vol. 908,
Issue. ,
Chen, J.G.
Cuvier, C.
Foucaut, J.-M.
Ostovan, Y.
and
Vassilicos, J.C.
2021.
A turbulence dissipation inhomogeneity scaling in the wake of two side-by-side square prisms.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Li, Sicheng
Long, Yanguang
and
Wang, Jinjun
2022.
Turbulent/non-turbulent interface for laminar boundary flow over a wall-mounted fence.
Physics of Fluids,
Vol. 34,
Issue. 12,
Long, Yanguang
Wang, Jiangsheng
and
Wang, Jinjun
2022.
“Turbulent/non-turbulent interface” in a low-Reynolds-number transitional boundary layer over a multi-element airfoil.
Physics of Fluids,
Vol. 34,
Issue. 10,
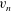 $v_{n}$ of the turbulent/non-turbulent interface and of the turbulence dissipation rate are closely related to each other in an axisymmetric and self-similar turbulent wake. The turbulence dissipation scaling implied by the Kolmogorov equilibrium cascade phenomenology is consistent with a Kolmogorov scaling of
$v_{n}$ of the turbulent/non-turbulent interface and of the turbulence dissipation rate are closely related to each other in an axisymmetric and self-similar turbulent wake. The turbulence dissipation scaling implied by the Kolmogorov equilibrium cascade phenomenology is consistent with a Kolmogorov scaling of 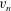 $v_{n}$ whereas the non-equilibrium dissipation scaling reported for various turbulent flows in Vassilicos (Annu. Rev. Fluid Mech., vol. 47, 2015, pp. 95–114), Dairay et al. (J. Fluid Mech., vol. 781, 2015, pp. 166–195), Goto & Vassilicos (Phys. Lett. A, vol. 379 (16), 2015, pp. 1144–1148) and Obligado et al. (Phys. Rev. Fluids, vol. 1 (4), 2016, 044409) is consistent with a different scaling of
$v_{n}$ whereas the non-equilibrium dissipation scaling reported for various turbulent flows in Vassilicos (Annu. Rev. Fluid Mech., vol. 47, 2015, pp. 95–114), Dairay et al. (J. Fluid Mech., vol. 781, 2015, pp. 166–195), Goto & Vassilicos (Phys. Lett. A, vol. 379 (16), 2015, pp. 1144–1148) and Obligado et al. (Phys. Rev. Fluids, vol. 1 (4), 2016, 044409) is consistent with a different scaling of  $v_{n}$ . We present results from a direct numerical simulation of a spatially developing axisymmetric and self-similar turbulent wake which supports this conclusion and the assumptions that it is based on.
$v_{n}$ . We present results from a direct numerical simulation of a spatially developing axisymmetric and self-similar turbulent wake which supports this conclusion and the assumptions that it is based on.

