Published online by Cambridge University Press: 08 August 2017
Turbulent mixing plays a major role in enabling the large-scale ocean circulation. The accuracy of mixing rates estimated from observations depends on our understanding of basic fluid mechanical processes underlying the nature of turbulence in a stratified fluid. Several of the key assumptions made in conventional mixing parameterizations have been increasingly scrutinized in recent years, primarily on the basis of adequately high resolution numerical simulations. We add to this evidence by compiling results from a suite of numerical simulations of the turbulence generated through stratified shear instability processes. We study the inherently intermittent and time-dependent nature of wave-induced turbulent life cycles and more specifically the tight coupling between inherently anisotropic scales upon which small-scale isotropic turbulence grows. The anisotropic scales stir and stretch fluid filaments enhancing irreversible diffusive mixing at smaller scales. We show that the characteristics of turbulent mixing depend on the relative time evolution of the Ozmidov length scale 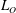 $L_{O}$ compared to the so-called Thorpe overturning scale
$L_{O}$ compared to the so-called Thorpe overturning scale 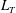 $L_{T}$ which represents the scale containing available potential energy upon which turbulence feeds and grows. We find that when
$L_{T}$ which represents the scale containing available potential energy upon which turbulence feeds and grows. We find that when 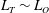 $L_{T}\sim L_{O}$, the mixing is most active and efficient since stirring by the largest overturns becomes ‘optimal’ in the sense that it is not suppressed by ambient stratification. We argue that the high mixing efficiency associated with this phase, along with observations of
$L_{T}\sim L_{O}$, the mixing is most active and efficient since stirring by the largest overturns becomes ‘optimal’ in the sense that it is not suppressed by ambient stratification. We argue that the high mixing efficiency associated with this phase, along with observations of 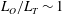 $L_{O}/L_{T}\sim 1$ in oceanic turbulent patches, together point to the potential for systematically underestimating mixing in the ocean if the role of overturns is neglected. This neglect, arising through the assumption of a clear separation of scales between the background mean flow and small-scale quasi-isotropic turbulence, leads to the exclusion of an highly efficient mixing phase from conventional parameterizations of the vertical transport of density. Such an exclusion may well be significant if the mechanism of shear-induced turbulence is assumed to be representative of at least some turbulent events in the ocean. While our results are based upon simulations of shear instability, we show that they are potentially more generic by making direct comparisons with
$L_{O}/L_{T}\sim 1$ in oceanic turbulent patches, together point to the potential for systematically underestimating mixing in the ocean if the role of overturns is neglected. This neglect, arising through the assumption of a clear separation of scales between the background mean flow and small-scale quasi-isotropic turbulence, leads to the exclusion of an highly efficient mixing phase from conventional parameterizations of the vertical transport of density. Such an exclusion may well be significant if the mechanism of shear-induced turbulence is assumed to be representative of at least some turbulent events in the ocean. While our results are based upon simulations of shear instability, we show that they are potentially more generic by making direct comparisons with 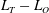 $L_{T}-L_{O}$ data from ocean and lake observations which represent a much wider range of turbulence-inducing physical processes.
$L_{T}-L_{O}$ data from ocean and lake observations which represent a much wider range of turbulence-inducing physical processes.