Hostname: page-component-5b777bbd6c-f9nfp Total loading time: 0 Render date: 2025-06-25T12:06:11.628Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-consistent model for active control of wind turbine wakes

Published online by Cambridge University Press:  23 June 2025

Zhaobin Li Open the ORCID record for Zhaobin Li [Opens in a new window]  and
Xiaolei Yang Open the ORCID record for Xiaolei Yang [Opens in a new window]
Zhaobin Li
Affiliation:
The State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, PR China
Xiaolei Yang*
Affiliation:
The State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, PR China
*
Corresponding author: Xiaolei Yang, xyang@imech.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

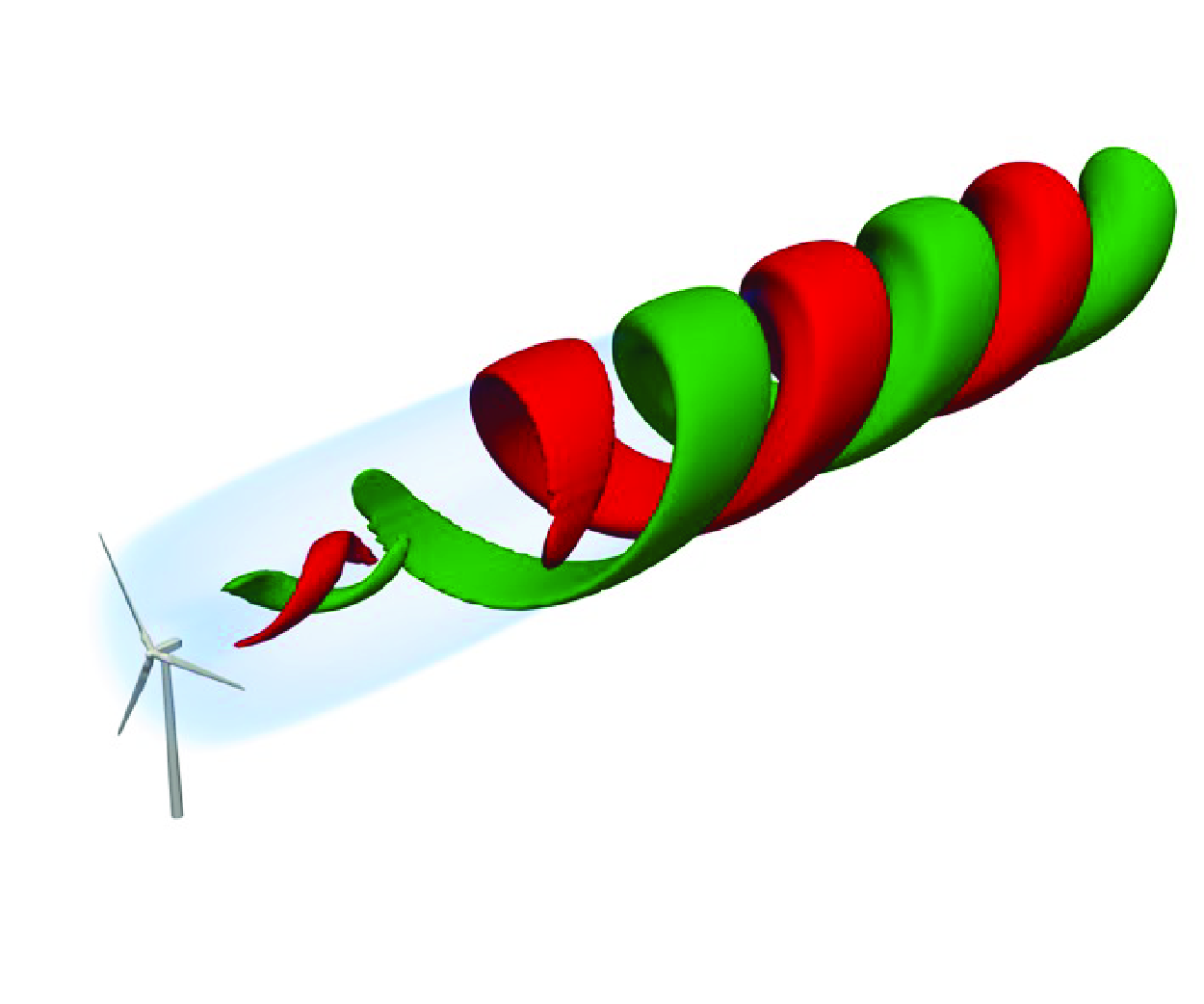
Active wake control (AWC) has emerged as a promising strategy for enhancing wind turbine wake recovery, but accurately modelling its underlying fluid mechanisms remains challenging. This study presents a computationally efficient wake model that provides end-to-end prediction capability from rotor actuation to wake recovery enhancement by capturing the coupled dynamics of wake meandering and mean flow modification, requiring only two inputs: a reference wake without control and a user-defined AWC strategy. The model combines physics-based resolvent modelling for large-scale coherent structures and an eddy viscosity modelling for small-scale turbulence. A Reynolds stress model is introduced to account for the influence of both coherent and incoherent wake fluctuations, so that the time-averaged wake recovery enhanced by the AWC can be quantitatively predicted. Validation against large-eddy simulations (LES) across various AWC approaches and actuating frequencies demonstrates the model’s predictive capability, accurately capturing AWC-specific and frequency-dependent mean wake recovery with less than 8 % error from LES while reducing computational time from thousands of central-processing-unit hours to minutes. The efficiency and accuracy of the model makes it a promising tool for practical AWC design and optimization of large-scale wind farms.

JFM classification

Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1013 , 25 June 2025 , A36
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abkar, M., Zehtabiyan-Rezaie, N. & Iosifidis, A. 2023 Reinforcement learning for wind-farm flow control: current state and future actions. Theor. Appl. Mech. Lett. 13 (6), 100475.Google Scholar
Ainslie, J.F. 1988 Calculating the flowfield in the wake of wind turbines. J. Wind Engng Indust Aerodyn. 27 (1–3), 213–224.10.1016/0167-6105(88)90037-2CrossRefGoogle Scholar
Bastankhah, M. & Porté-Agel, F. 2014 A new analytical model for wind-turbine wakes. Renew. Energy 70, 116–123.10.1016/j.renene.2014.01.002CrossRefGoogle Scholar
Bastankhah, M. & Porté-Agel, F. 2016 Experimental and theoretical study of wind turbine wakes in yawed conditions. J. Fluid Mech. 806, 506–541.10.1017/jfm.2016.595CrossRefGoogle Scholar
Bir, G. 2008 Multi-blade coordinate transformation and its application to wind turbine analysis. In 46th AIAA aerospace sciences meeting and exhibit, pp. 1300.Google Scholar
Biswas, N. & Buxton, O.R.H. 2024 Energy exchanges between coherent modes in the near wake of a wind turbine model at different tip speed ratios. J. Fluid Mech. 996, A8.10.1017/jfm.2024.581CrossRefGoogle Scholar
Bortolotti, P., Tarres, H.C., Dykes, K.L., Merz, K., Sethuraman, L., Verelst, D. & Zahle, F. 2019 IEA Wind TCP Task 37: Systems engineering in wind energy-WP2. 1 Reference wind turbines. Tech. Rep, National Renewable Energy Lab.(NREL),Google Scholar
Cheung, L.C., Brown, K.A., Houck, D.R. & Develder, N.B. 2024 Fluid-dynamic mechanisms underlying wind turbine wake control with strouhal-timed actuation. Energies 17 (4), 865.10.3390/en17040865CrossRefGoogle Scholar
Chorin, A.J. 1967 The numerical solution of the Navier-Stokes equations for an incompressible fluid. Bull. Am. Math. Soc. 73 (6), 928–931.10.1090/S0002-9904-1967-11853-6CrossRefGoogle Scholar
De Cillis, G., Cherubini, S., Semeraro, O., Leonardi, S. & De Palma, P. 2022 Stability and optimal forcing analysis of a wind turbine wake: Comparison with POD. Renew. Energy 181, 765–785.CrossRefGoogle Scholar
Dong, G., Qin, J., Li, Z. & Yang, X. 2023 Characteristics of wind turbine wakes for different blade designs. J. Fluid Mech. 847, 821–867.Google Scholar
Eguinoa, I., Göçmen, T., Garcia‐Rosa, P.B., Das, K., Petrović, V., Kölle, K., Manjock, A., Koivisto, M.J. & Smailes, M. 2021 Wind farm flow control oriented to electricity markets and grid integration: initial perspective analysis. Adv. Control Appl. Engng Indust. Syst. 3 (3), e80.10.1002/adc2.80CrossRefGoogle Scholar
Feng, D., Gupta, V., Li, L.K.B. & Wan, M. 2024 An improved dynamic model for wind-turbine wake flow. Energy 290, 130167.10.1016/j.energy.2023.130167CrossRefGoogle Scholar
Feng, D., Li, L.K.B., Gupta, V. & Wan, M. 2022 Componentwise influence of upstream turbulence on the far-wake dynamics of wind turbines. Renew. Energy 200, 1081–1091.10.1016/j.renene.2022.10.024CrossRefGoogle Scholar
Fontanella, A., Bayati, I., Mikkelsen, R., Belloli, M. & Zasso, A. 2021 UNAFLOW: a holistic wind tunnel experiment about the aerodynamic response of floating wind turbines under imposed surge motion. Wind Energy Sci. 6 (5), 1169–1190.10.5194/wes-6-1169-2021CrossRefGoogle Scholar
Foti, D., Yang, X. & Sotiropoulos, F. 2018 Similarity of wake meandering for different wind turbine designs for different scales. J. Fluid Mech. 842, 5–25.CrossRefGoogle Scholar
Frederik, J.A., Doekemeijer, B.M., Mulders, S.P. & van Wingerden, J‐W. 2020 The helix approach: using dynamic individual pitch control to enhance wake mixing in wind farms. Wind Energy 23 (8), 1739–1751.10.1002/we.2513CrossRefGoogle Scholar
Fu, S.F., Jin, Y.Q., Zheng, Y. & Chamorro, L.P. 2019 Wake and power fluctuations of a model wind turbine subjected to pitch and roll oscillations. Appl. Energ. 253, 113605.10.1016/j.apenergy.2019.113605CrossRefGoogle Scholar
Gambuzza, S. & Ganapathisubramani, B. 2023 The influence of free stream turbulence on the development of a wind turbine wake. J. Fluid Mech. 963, A19.10.1017/jfm.2023.302CrossRefGoogle Scholar
Ge, L. & Sotiropoulos, F. 2007 A numerical method for solving the 3D unsteady incompressible Navier–Stokes equations in curvilinear domains with complex immersed boundaries. J. Comput. Phys. 225 (2), 1782–1809.10.1016/j.jcp.2007.02.017CrossRefGoogle ScholarPubMed
Germano, M., Piomelli, U., Moin, P. & Cabot, W.H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A: Fluid Dyn. 3 (7), 1760–1765.10.1063/1.857955CrossRefGoogle Scholar
Goit, J.P. & Meyers, J. 2015 Optimal control of energy extraction in wind-farm boundary layers. J. Fluid Mech. 768, 5–50.10.1017/jfm.2015.70CrossRefGoogle Scholar
Gupta, V. & Wan, M. 2019 Low-order modelling of wake meandering behind turbines. J. Fluid Mech. 877, 534–560.10.1017/jfm.2019.619CrossRefGoogle Scholar
Ho, C.-M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16 (1), 365–424.10.1146/annurev.fl.16.010184.002053CrossRefGoogle Scholar
van der Hoek, D., den Abbeele, B.V., Simao Ferreira, C. & van Wingerden, J‐W. 2024 Maximizing wind farm power output with the helix approach: experimental validation and wake analysis using tomographic particle image velocimetry. Wind Energy 27 (5), 463–482.10.1002/we.2896CrossRefGoogle Scholar
Houck, D.R. 2022 Review of wake management techniques for wind turbines. Wind Energy 25 (2), 195–220.10.1002/we.2668CrossRefGoogle Scholar
Howland, M.F., Quesada, J.A.B., Martínez, J.J.P., Larrañaga, F.P., Yadav, N., Chawla, J.S., Sivaram, V. & Dabiri, J.O. 2022 Collective wind farm operation based on a predictive model increases utility-scale energy production. Nature Energy 7 (9), 818–827.10.1038/s41560-022-01085-8CrossRefGoogle Scholar
Hussain, A.K.M.F. & Reynolds, W.C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41 (2), 241–258.CrossRefGoogle Scholar
Iungo, G.V., Viola, F., Camarri, S., Porté-Agel, F. & Gallaire, F. 2013 Linear stability analysis of wind turbine wakes performed on wind tunnel measurements. J. Fluid Mech. 737, 499–526.Google Scholar
Kaplan, O., Jordan, P., Cavalieri, A.V.G. & Brès, G.A. 2021 Nozzle dynamics and wavepackets in turbulent jets. J. Fluid Mech. 923, A22.10.1017/jfm.2021.566CrossRefGoogle Scholar
Kheirabadi, A.C. & Nagamune, R. 2019 A quantitative review of wind farm control with the objective of wind farm power maximization. J. Wind Engng Indust. Aerodyn. 192, 45–73.CrossRefGoogle Scholar
Kleusberg, E., Benard, S. & Henningson, D.S. 2019 Tip-vortex breakdown of wind turbines subject to shear. Wind Energy 22 (12), 1789–1799.10.1002/we.2403CrossRefGoogle Scholar
Kopperstad, K.M., Kumar, R. & Shoele, K. 2020 Aerodynamic characterization of barge and spar type floating offshore wind turbines at different sea states. Wind Energy 23 (11), 2087–2112.CrossRefGoogle Scholar
Korb, H., Asmuth, H. & Ivanell, S. 2023 The characteristics of helically deflected wind turbine wakes. J. Fluid Mech. 965, A2.10.1017/jfm.2023.390CrossRefGoogle Scholar
Larsen, G.C., Madsen, H.A., Thomsen, K. & Larsen, T.J. 2008 Wake meandering: a pragmatic approach. Wind Energy: Intl J. Prog. Appl. Wind Power Conversion Technol. 11 (4), 377–395.10.1002/we.267CrossRefGoogle Scholar
Li, B., Ge, M., Li, X. & Liu, Y. 2024 a A physics-guided machine learning framework for real-time dynamic wake prediction of wind turbines. Phys. Fluids 36 (3), 035143.10.1063/5.0194764CrossRefGoogle Scholar
Li, Y., Zhang, F., Li, Z. & Yang, X. 2024 b Impacts of inflow turbulence on the flow past a permeable disk. J. Fluid Mech. 999, A30.10.1017/jfm.2024.876CrossRefGoogle Scholar
Li, Z., Dong, G. & Yang, X. 2022 Onset of wake meandering for a floating offshore wind turbine under side-to-side motion. J. Fluid Mech. 934, A29.10.1017/jfm.2021.1147CrossRefGoogle Scholar
Li, Z. & Yang, X. 2021 Large-eddy simulation on the similarity between wakes of wind turbines with different yaw angles. J. Fluid Mech. 921, A11.10.1017/jfm.2021.495CrossRefGoogle Scholar
Li, Z. & Yang, X. 2024 Resolvent-based motion-to-wake modelling of wind turbine wakes under dynamic rotor motion. J. Fluid Mech. 980, A48.10.1017/jfm.2023.1097CrossRefGoogle Scholar
Lin, M. & Porté-Agel, F. 2022 Large-eddy simulation of a wind-turbine array subjected to active yaw control. Wind Energy Sci. 7 (6), 2215–2230.10.5194/wes-7-2215-2022CrossRefGoogle Scholar
Lin, M. & Porté-Agel, F. 2024 Wake meandering of wind turbines under dynamic yaw control and impacts on power and fatigue. Renew. Energy 223, 120003.10.1016/j.renene.2024.120003CrossRefGoogle Scholar
Mantič-Lugo, V., Arratia, C. & Gallaire, F. 2014 Self-consistent mean flow description of the nonlinear saturation of the vortex shedding in the cylinder wake. Phys. Rev. Lett. 113 (8), 084501.10.1103/PhysRevLett.113.084501CrossRefGoogle ScholarPubMed
Mao, X. & Sørensen, J.N. 2018 Far-wake meandering induced by atmospheric eddies in flow past a wind turbine. J. Fluid Mech. 846, 190–209.10.1017/jfm.2018.275CrossRefGoogle Scholar
Martini, E., Rodríguez, D., Towne, A. & Cavalieri, A.V.G. 2021 Efficient computation of global resolvent modes. J. Fluid Mech. 919, A3.Google Scholar
McKeon, B.J. & Sharma, A.S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.10.1017/S002211201000176XCrossRefGoogle Scholar
Meneveau, C. 2024 The fluid mechanics of active flow control at very large scales. J. Fluid Mech. 1000, F9.CrossRefGoogle Scholar
Messmer, T., Hölling, M. & Peinke, J. 2024 Enhanced recovery caused by nonlinear dynamics in the wake of a floating offshore wind turbine. J. Fluid Mech. 984, A66.10.1017/jfm.2024.175CrossRefGoogle Scholar
Meyers, J., Bottasso, C., Dykes, K., Fleming, P., Gebraad, P., Giebel, G., Göçmen, T. & van Wingerden, J.W. 2022 Wind farm flow control: prospects and challenges. Wind Energy Sci. 7 (6), 2271–2306.Google Scholar
Munters, W. & Meyers, J. 2017 An optimal control framework for dynamic induction control of wind farms and their interaction with the atmospheric boundary layer. Phil. Trans. R. Society A: Math. Phys. Engng Sci. 375 (2091), 20160100.10.1098/rsta.2016.0100CrossRefGoogle ScholarPubMed
Munters, W. & Meyers, J. 2018 Dynamic strategies for yaw and induction control of wind farms based on large-eddy simulation and optimization. Energies 11 (1), 177.10.3390/en11010177CrossRefGoogle Scholar
Pickering, E., Rigas, G., Schmidt, O.T., Sipp, D. & Colonius, T. 2021 Optimal eddy viscosity for resolvent-based models of coherent structures in turbulent jets. J. Fluid Mech. 917, A29.Google Scholar
Porté-Agel, F., Bastankhah, M. & Shamsoddin, S. 2020 Wind-turbine and wind-farm flows: a review. Boundary-layer Meteorol. 174 (1), 1–59.10.1007/s10546-019-00473-0CrossRefGoogle ScholarPubMed
Ribeiro, J.H.M., Yeh, C.-A. & Taira, K. 2020 Randomized resolvent analysis. Phys. Rev. Fluids 5 (3), 033902.10.1103/PhysRevFluids.5.033902CrossRefGoogle Scholar
Rolandi, L.V., Ribeiro, J.H.M., Yeh, C.-A. & Taira, K. 2024 An invitation to resolvent analysis. Theor. Comput. Fluid Dyn. 38 (5), 1–37.10.1007/s00162-024-00717-xCrossRefGoogle Scholar
Schmid, P.J. & Henningson, D.S. 2001 Stability and transition in shear flows. Applied Mathematical Sciences, vol. 142. Springer.Google Scholar
Shapiro, C.R., Gayme, D.F. & Meneveau, C. 2018 Modelling yawed wind turbine wakes: a lifting line approach. J. Fluid Mech. 841, R1.10.1017/jfm.2018.75CrossRefGoogle Scholar
Shapiro, C.R., Starke, G.M. & Gayme, D.F. 2022 Turbulence and control of wind farms. Annu. Rev. Control Robot. Autonom. Syst. 5 (1), 579–602.10.1146/annurev-control-070221-114032CrossRefGoogle Scholar
Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open-flows: a linearized approach. Appl. Mech. Rev. 63 (3), 030801.10.1115/1.4001478CrossRefGoogle Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations: i. the basic experiment. Mon. Weather Rev. 91 (3), 99–164.10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;22.3.CO;2>CrossRefGoogle Scholar
Stevens, R.J.A.M. & Meneveau, C. 2017 Flow structure and turbulence in wind farms. Annu. Rev. Fluid Mech. 49 (1), 311–339.10.1146/annurev-fluid-010816-060206CrossRefGoogle Scholar
Symon, S., Madhusudanan, A., Illingworth, S.J. & Marusic, I. 2023 Use of eddy viscosity in resolvent analysis of turbulent channel flow. Phys. Rev. Fluids 8 (6), 064601.10.1103/PhysRevFluids.8.064601CrossRefGoogle Scholar
Towne, A., Rigas, G., Kamal, O., Pickering, E. & Colonius, T. 2022 Efficient global resolvent analysis via the one-way Navier–Stokes equations. J. Fluid Mech. 948, A9.10.1017/jfm.2022.647CrossRefGoogle Scholar
Tran, T.T. & Kim, D.H. 2015 The aerodynamic interference effects of a floating offshore wind turbine experiencing platform pitching and yawing motions. J. Mech. Sci. Technol. 29 (2), 549–561.10.1007/s12206-015-0115-0CrossRefGoogle Scholar
Trefethen, L.N., Trefethen, A.E., Reddy, S.C. & Driscoll, T.A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.10.1126/science.261.5121.578CrossRefGoogle ScholarPubMed
Vermeer, L.J., Sørensen, J.N. & Crespo, A. 2003 Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 39 (6–7), 467–510.10.1016/S0376-0421(03)00078-2CrossRefGoogle Scholar
Wang, K., Zhao, M., Chen, S. & Zha, R. 2024 Aerodynamic performance analysis of a floating wind turbine with coupled blade rotation and surge motion. Engng Appl. Comput. Fluid 18 (1), 2301524.Google Scholar
Wei, N.J. & Dabiri, J.O. 2023 Power-generation enhancements and upstream flow properties of turbines in unsteady inflow conditions. J. Fluid Mech. 966, A30.10.1017/jfm.2023.454CrossRefGoogle Scholar
Wei, N.J., El Makdah, A., Hu, J.C., Kaiser, F., Rival, D.E. & Dabiri, J.O. 2024 Wake dynamics of wind turbines in unsteady streamwise flow conditions. J. Fluid Mech. 1000, A66.10.1017/jfm.2024.999CrossRefGoogle Scholar
Wu, T. & He, G. 2023 Composition of resolvents enhanced by random sweeping for large-scale structures in turbulent channel flows. J. Fluid Mech. 956, A31.10.1017/jfm.2023.39CrossRefGoogle Scholar
Wu, X. 2019 Nonlinear theories for shear flow instabilities: physical insights and practical implications. Annu. Rev. Fluid Mech. 51 (1), 451–485.10.1146/annurev-fluid-122316-045252CrossRefGoogle Scholar
Yang, X., Hong, J., Barone, M. & Sotiropoulos, F. 2016 Coherent dynamics in the rotor tip shear layer of utility-scale wind turbines. J. Fluid Mech. 804, 90–115.10.1017/jfm.2016.503CrossRefGoogle Scholar
Yang, X. & Sotiropoulos, F. 2018 A new class of actuator surface models for wind turbines. Wind Energy 21 (5), 285–302.10.1002/we.2162CrossRefGoogle Scholar
Yang, X., Sotiropoulos, F., Conzemius, R.J., Wachtler, J.N. & Strong, M.B. 2015 Large-eddy simulation of turbulent flow past wind turbines/farms: the Virtual Wind Simulator (VWiS). Wind Energy 18 (12), 2025–2045.10.1002/we.1802CrossRefGoogle Scholar
Yang, X., Zhang, X., Li, Z. & He, G.-W. 2009 A smoothing technique for discrete delta functions with application to immersed boundary method in moving boundary simulations. J. Comput. Phys. 228 (20), 7821–7836.10.1016/j.jcp.2009.07.023CrossRefGoogle Scholar
Yim, E., Meliga, P. & Gallaire, F. 2019 Self-consistent triple decomposition of turbulent flow over a backward-facing step under harmonic forcing. Proc. R. Soc. A 475 (2225), 20190018.10.1098/rspa.2019.0018CrossRefGoogle Scholar