Hostname: page-component-84b7d79bbc-tsvsl Total loading time: 0 Render date: 2024-07-27T09:25:49.672Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-sustaining process of minimal attached eddies in turbulent channel flow

Published online by Cambridge University Press:  20 April 2016

Yongyun Hwang  and
Yacine Bengana
Yongyun Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
Yacine Bengana
Affiliation:
Départment de Mécanique, Université de Pierre et Marie Curie, 4 Place Jussieu, 75005 Paris, France
*
†Email address for correspondence: y.hwang@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

It has been recently shown that the energy-containing motions (i.e. coherent structures) in turbulent channel flow exist in the form of Townsend’s attached eddies by a numerical experiment which simulates the energy-containing motions only at a prescribed spanwise length scale using their self-sustaining nature (Hwang, J. Fluid Mech., vol. 767, 2015, pp. 254–289). In the present study, a detailed investigation of the self-sustaining process of the energy-containing motions at each spanwise length scale (i.e. the attached eddies) in the logarithmic and outer regions is carried out with an emphasis on its relevance to ‘bursting’, which refers to an energetic temporal oscillation of the motions (Flores & Jiménez, Phys. Fluids, vol. 22, 2010, 071704). It is shown that the attached eddies in the logarithmic and outer regions, composed of streaks and quasi-streamwise vortical structures, bear the self-sustaining process remarkably similar to that in the near-wall region: i.e. the streaks are significantly amplified by the quasi-streamwise vortices via the lift-up effect; the amplified streaks subsequently undergo a ‘rapid streamwise meandering motion’, reminiscent of streak instability or transient growth, which eventually results in breakdown of the streaks and regeneration of new quasi-streamwise vortices. For the attached eddies at a given spanwise length scale 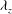${\it\lambda}_{z}$ between 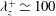${\it\lambda}_{z}^{+}\simeq 100$ and 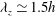${\it\lambda}_{z}\simeq 1.5h$, the single turnover time period of the self-sustaining process is found to be 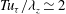$Tu_{{\it\tau}}/{\it\lambda}_{z}\simeq 2$ (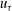$u_{{\it\tau}}$ is the friction velocity), which corresponds well to the time scale of the bursting. Two additional numerical experiments, designed to artificially suppress the lift-up effect and the streak meandering motions, respectively, reveal that these processes are essential ingredients of the self-sustaining process of the attached eddies in the logarithmic and outer regions, consistent with several previous theoretical studies. It is also shown that the artificial suppression of the lift-up effect of the attached eddies in the logarithmic and outer regions leads to substantial amounts of turbulent skin-friction reduction.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 708 - 738
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4, 1637–1650.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flow. Phys. Fluids 5, 774–777.Google Scholar
Chernyshenko, S. I. & Baig, M. F. 2005 The mechanism of streak formation in near-wall turbulence. J. Fluid. Mech. 544, 99–131.CrossRefGoogle Scholar
Cossu, C. & Brandt, L. 2002 Stabilization of Tollmien–Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 14, L57–L60.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18, 487–488.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Travelling waves in pipe flow. Phys. Rev. Lett. 91, 224502.CrossRefGoogle ScholarPubMed
Flores, O. & Jiménez, J 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Gustavsson, L. H. 1991 Energy growth of three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 224, 241–260.CrossRefGoogle Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Härtel, C. & Kleiser, L. 1998 Analysis and modelling of subgrid-scale motions in near-wall turbulence. J. Fluid Mech. 356, 327–352.Google Scholar
Hœpffner, J., Brandt, L. & Henningson, D. S. 2005 Transient growth on boundary layer streaks. J. Fluid Mech. 537, 91–100.Google Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.Google Scholar
Hwang, Y. & Cossu, C. 2010a Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010b Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Hwang, Y. & Cossu, C. 2010c Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105, 044505.CrossRefGoogle ScholarPubMed
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23, 061702.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Jiménez, J. 2013 How linear is wall-bounded turbulence. Phys. Fluids 25, 110814.Google Scholar
Jiménez, J. 2015 Direct detection of linearized bursts in turbulence. Phys. Fluids 27, 065102.Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Jiménez, J., Kawahara, G., Simens, M. P., Nagata, M. & Shiba, M. 2005 Phys. Fluids 17, 015105.CrossRefGoogle Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.Google Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.CrossRefGoogle Scholar
Kim, J. & Lim, J. 2000 A linear process in wall-bounded turbulent shear flows. Phys. Fluids 12 (8), 1885–1888.CrossRefGoogle Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
Landahl, M. T. 1990 On sublayer streaks. J. Fluid Mech. 212, 593–614.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re = 4200. Phys. Fluids 26, 011702.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulent intensity formulation for flat-flate boundary layers. Phys. Fluids 15 (8), 2461.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mason, P. J. & Cullen, N. J. 1986 On the magnitude of the subgrid-scale eddy coefficient in large-eddy simulations of turbulent channel flow. J. Fluid Mech. 162, 439–462.Google Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k - 1 law in a high Reynolds number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.Google Scholar
Orlandi, P., Bernardini, M. & Pirozzoli, S. 2015 Poiseuille and couette flows in the transitional and fully turbulent regime. J. Fluid Mech. 770, 424–441.CrossRefGoogle Scholar
Park, D. S. & Huerre, P. 1995 Primary and secondary instabilities of the asymptotic suction boundary layer on a curved plate. J. Fluid Mech. 283, 249–272.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in the turbulent Couette and Poiseulle flows. C. R. Méc 339 (1), 1–5.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1: extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.CrossRefGoogle Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11 (1), 97–120.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Hwang, Y. & Cossu, C. 2010 Optimally amplified large-scale streaks and drag reduction in the turbulent pipe flow. Phys. Rev. E 82, 036321.Google Scholar