Article contents
Separation control and drag reduction for boat-tailed axisymmetric bodies through contoured transverse grooves
Published online by Cambridge University Press: 26 October 2017
Abstract
We describe the results of a numerical and experimental investigation aimed at assessing the performance of a control method to delay boundary layer separation consisting of the introduction on the surface of contoured transverse grooves, i.e. of small cavities with an appropriate shape orientated transverse to the incoming flow. The shape of the grooves and their depth – which must be significantly smaller than the thickness of the incoming boundary layer – are chosen so that the flow recirculations present within the grooves are steady and stable. This passive control strategy is applied to an axisymmetric bluff body with various rear boat tails, which are characterized by different degrees of flow separation. Variational multiscale large eddy simulations and wind tunnel tests are carried out. The Reynolds number, for both experiments and simulations, is 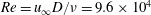 $Re=u_{\infty }D/\unicode[STIX]{x1D708}=9.6\times 10^{4}$ ; due to the different incoming flow turbulence level, the boundary layer conditions before the boat tails are fully developed turbulent in the experiments and transitional in the simulations. In all cases, the introduction of one single axisymmetric groove in the lateral surface of the boat tails produces significant delay of the boundary layer separation, with consequent reduction of the pressure drag. Nonetheless, the wake dynamical structure remains qualitatively similar to the one typical of a blunt-based axisymmetric body, with quantitative variations that are consistent with the reduction in wake width caused by boat tailing and by the grooves. A few supplementary simulations show that the effect of the grooves is also robust to the variation of the geometrical parameters defining their shape. All the obtained data support the interpretation that the relaxation of the no-slip boundary condition for the flow surrounding the recirculation regions, with an appreciable velocity along their borders, is the physical mechanism responsible for the effectiveness of the present separation-control method.
$Re=u_{\infty }D/\unicode[STIX]{x1D708}=9.6\times 10^{4}$ ; due to the different incoming flow turbulence level, the boundary layer conditions before the boat tails are fully developed turbulent in the experiments and transitional in the simulations. In all cases, the introduction of one single axisymmetric groove in the lateral surface of the boat tails produces significant delay of the boundary layer separation, with consequent reduction of the pressure drag. Nonetheless, the wake dynamical structure remains qualitatively similar to the one typical of a blunt-based axisymmetric body, with quantitative variations that are consistent with the reduction in wake width caused by boat tailing and by the grooves. A few supplementary simulations show that the effect of the grooves is also robust to the variation of the geometrical parameters defining their shape. All the obtained data support the interpretation that the relaxation of the no-slip boundary condition for the flow surrounding the recirculation regions, with an appreciable velocity along their borders, is the physical mechanism responsible for the effectiveness of the present separation-control method.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 62
- Cited by


