Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-29T17:33:33.942Z Has data issue: false hasContentIssue false
  • English
  • Français

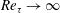Shear stress-driven flow: the state space of near-wall turbulence as $Re_{\unicode[STIX]{x1D70F}}\rightarrow \infty$

Published online by Cambridge University Press:  11 July 2019

Patrick Doohan Open the ORCID record for Patrick Doohan [Opens in a new window] ,
Ashley P. Willis Open the ORCID record for Ashley P. Willis [Opens in a new window]  and
Yongyun Hwang Open the ORCID record for Yongyun Hwang [Opens in a new window]
Patrick Doohan*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
Ashley P. Willis
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK
Yongyun Hwang
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: patrick.doohan15@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

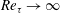An inner-scaled, shear stress-driven flow is considered as a model of independent near-wall turbulence as the friction Reynolds number $Re_{\unicode[STIX]{x1D70F}}\rightarrow \infty$. In this limit, the model is applicable to the near-wall region and the lower part of the logarithmic layer of various parallel shear flows, including turbulent Couette flow, Poiseuille flow and Hagen–Poiseuille flow. The model is validated against damped Couette flow and there is excellent agreement between the velocity statistics and spectra for the wall-normal height 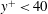$y^{+}<40$. A near-wall flow domain of similar size to the minimal unit is analysed from a dynamical systems perspective. The edge and fifteen invariant solutions are computed, the first discovered for this flow configuration. Through continuation in the spanwise width 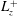$L_{z}^{+}$, the bifurcation behaviour of the solutions over the domain size is investigated. The physical properties of the solutions are explored through phase portraits, including the energy input and dissipation plane, and streak, roll and wave energy space. Finally, a Reynolds number is defined in outer units and the high-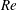$Re$ asymptotic behaviour of the equilibria is studied. Three lower branch solutions are found to scale consistently with vortex–wave interaction (VWI) theory, with wave forcing localising around the critical layer.

JFM classification

Turbulent Flows: Turbulent Flows Nonlinear Dynamical Systems: Nonlinear Dynamical Systems
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 606 - 638
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Ingenieur-Archiv 52 (6), 355–377.Google Scholar
Afzal, N. 1984 Mesolayer theory for turbulent flows. AIAA J. 22 (3), 437–439.Google Scholar
Agostini, L. & Leschziner, M. 2016 Predicting the response of small-scale near-wall turbulence to large-scale outer motions. Phys. Fluids 28 (1), 015107.Google Scholar
Barkley, D. 2016 Theoretical perspective on the route to turbulence in a pipe. J. Fluid Mech. 803, P1.Google Scholar
Bewley, T. R. 2014 Numerical Renaissance: Simulation, Optimization and Control. Renaissance Press.Google Scholar
Budanur, N. B., Short, K. Y., Farazmand, M., Willis, A. P. & Cvitanović, P. 2017 Relative periodic orbits form the backbone of turbulent pipe flow. J. Fluid Mech. 833, 274–301.Google Scholar
Cassinelli, A., de Giovanetti, M. & Hwang, Y. 2017 Streak instability in near-wall turbulence revisited. J. Turbul. 18 (5), 443–464.Google Scholar
Cho, M., Hwang, Y. & Choi, H. 2018 Scale interactions and spectral energy transfer in turbulent channel flow. J. Fluid Mech. 854, 474–504.Google Scholar
Deguchi, K. 2015 Self-sustained states at Kolmogorov microscale. J. Fluid Mech. 781, R6.Google Scholar
Deguchi, K., Hall, P. & Walton, A. 2013 The emergence of localized vortex–wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.Google Scholar
Eckhardt, B. & Zammert, S. 2018 Small scale exact coherent structures at large Reynolds numbers in plane Couette flow. Nonlinearity 31 (2), R66.Google Scholar
Faller, A. J. 1971 Oceanic turbulence and the Langmuir circulations. Annu. Rev. Ecol. Systematics 2 (1), 201–236.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
de Giovanetti, M., Sung, H. J. & Hwang, Y. 2017 Streak instability in turbulent channel flow: the seeding mechanism of large-scale motions. J. Fluid Mech. 832, 483–513.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.Google Scholar
Hwang, Y. 2016 Mesolayer of attached eddies in turbulent channel flow. Phys. Rev. Fluids 1 (6), 064401.Google Scholar
Hwang, Y. & Bengana, Y. 2016 Self-sustaining process of minimal attached eddies in turbulent channel flow. J. Fluid Mech. 795, 708–738.Google Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.Google Scholar
Hwang, Y., Willis, A. P. & Cossu, C. 2016 Invariant solutions of minimal large-scale structures in turbulent channel flow for Re 𝜏 up to 1000. J. Fluid Mech. 802, R1.Google Scholar
Jiménez, J., Del Alamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.Google Scholar
Jiménez, J., Kawahara, G., Simens, M. P., Nagata, M. & Shiba, M. 2005 Characterization of near-wall turbulence in terms of equilibrium and ‘bursting’ solutions. Phys. Fluids 17 (1), 015105.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Jiménez, J. & Simens, M. P. 2001 Low-dimensional dynamics of a turbulent wall flow. J. Fluid Mech. 435, 81–91.Google Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.Google Scholar
Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in turbulent channel flow. Phys. Fluids A 5 (3), 695–706.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41 (2), 283–325.Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.Google Scholar
Leibovich, S. 1983 The form and dynamics of Langmuir circulations. Annu. Rev. Fluid Mech. 15 (1), 391–427.Google Scholar
Long, R. R. & Chen, T.-C. 1981 Experimental evidence for the existence of the ‘mesolayer’ in turbulent systems. J. Fluid Mech. 105, 19–59.Google Scholar
Lucas, D. & Kerswell, R. 2017 Sustaining processes from recurrent flows in body-forced turbulence. J. Fluid Mech. 817, R3.Google Scholar
Lustro, J. R. T., Kawahara, G., van Veen, L., Shimizu, M. & Kokubu, H. 2019 The onset of transient turbulence in minimal plane Couette flow. J. Fluid Mech. 862, R2.Google Scholar
Marusic, I., Baars, W. J. & Hutchins, N. 2017 Scaling of the streamwise turbulence intensity in the context of inner-outer interactions in wall turbulence. Phys. Rev. Fluids 2 (10), 100502.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Orszag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50 (4), 689–703.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Romanov, V. A. 1973 Stability of plane-parallel Couette flow. Funct. Anal. Appl. 7 (2), 137–146.Google Scholar
Schneider, T. M., Eckhardt, B. & Yorke, J. A. 2007 Turbulence transition and the edge of chaos in pipe flow. Phys. Rev. Lett. 99 (3), 034502.Google Scholar
Schneider, T. M., Gibson, J. F., Lagha, M., De Lillo, F. & Eckhardt, B. 2008 Laminar-turbulent boundary in plane Couette flow. Phys. Rev. E 78 (3), 037301.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Sekimoto, A., Dong, S. & Jiménez, J. 2016 Direct numerical simulation of statistically stationary and homogeneous shear turbulence and its relation to other shear flows. Phys. Fluids 28 (3), 035101.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96 (17), 174101.Google Scholar
Sreenivasan, K. R. & Sahay, A. 1997 The persistence of viscous effects in the overlap region, and the mean velocity in turbulent pipe and channel flows. In Self-Sustaining Mechanisms of Wall Turbulence (ed. Panton, R.), pp. 253–272. Computational Mechanics Publications.Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Thorpe, S. A. 2004 Langmuir circulation. Annu. Rev. Fluid Mech. 36, 55–79.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1980 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
Viswanath, D. 2009 The critical layer in pipe flow at high Reynolds number. Phil. Trans. R. Soc. Lond. A 367 (1888), 561–576.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.Google Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81 (19), 4140.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15 (6), 1517–1534.Google Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Willis, A. P., Cvitanović, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.Google Scholar
Yang, Q., Willis, A. P. & Hwang, Y. 2018 Energy production and self-sustained turbulence at the kolmogorov scale in Couette flow. J. Fluid Mech. 834, 531–554.Google Scholar
Yang, Q., Willis, A. P. & Hwang, Y. 2019 Exact coherent states of attached eddies in channel flow. J. Fluid Mech. 862, 1029–1059.Google Scholar