Article contents
Shear-induced breaking of large internal solitary waves
Published online by Cambridge University Press: 10 February 2009
Abstract
The stability properties of 24 experimentally generated internal solitary waves (ISWs) of extremely large amplitude, all with minimum Richardson number less than 1/4, are investigated. The study is supplemented by fully nonlinear calculations in a three-layer fluid. The waves move along a linearly stratified pycnocline (depth h2) sandwiched between a thin upper layer (depth h1) and a deep lower layer (depth h3), both homogeneous. In particular, the wave-induced velocity profile through the pycnocline is measured by particle image velocimetry (PIV) and obtained in computation. Breaking ISWs were found to have amplitudes (a1) in the range 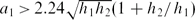 , while stable waves were on or below this limit. Breaking ISWs were investigated for 0.27 < h2/h1 < 1 and 4.14 < h3/(h1 + h2) < 7.14 and stable waves for 0.36 < h2/h1 < 3.67 and 3.22 < h3/(h1 + h2) < 7.25. Kelvin–Helmholtz-like billows were observed in the breaking cases. They had a length of 7.9h2 and a propagation speed 0.09 times the wave speed. These measured values compared well with predicted values from a stability analysis, assuming steady shear flow with U(z) and ρ(z) taken at the wave maximum (U(z) horizontal velocity profile, ρ(z) density along the vertical z). Only unstable modes in waves of sufficient strength have the chance to grow sufficiently fast to develop breaking: the waves that broke had an estimated growth (of unstable modes) more than 3.3–3.7 times than in the strongest stable case. Evaluation of the minimum Richardson number (Rimin, in the pycnocline), the horizontal length of a pocket of possible instability, with wave-induced Ri < 14, (Lx) and the wavelength (λ), showed that all measurements fall within the range Rimin = −0.23Lx/λ + 0.298 ± 0.016 in the (Lx/λ, Rimin)-plane. Breaking ISWs were found for Lx/λ > 0.86 and stable waves for Lx/λ < 0.86. The results show a sort of threshold-like behaviour in terms of Lx/λ. The results demonstrate that the breaking threshold of Lx/λ = 0.86 was sharper than one based on a minimum Richardson number and reveal that the Richardson number was found to become almost antisymmetric across relatively thick pycnoclines, with the minimum occurring towards the top part of the pycnocline.
, while stable waves were on or below this limit. Breaking ISWs were investigated for 0.27 < h2/h1 < 1 and 4.14 < h3/(h1 + h2) < 7.14 and stable waves for 0.36 < h2/h1 < 3.67 and 3.22 < h3/(h1 + h2) < 7.25. Kelvin–Helmholtz-like billows were observed in the breaking cases. They had a length of 7.9h2 and a propagation speed 0.09 times the wave speed. These measured values compared well with predicted values from a stability analysis, assuming steady shear flow with U(z) and ρ(z) taken at the wave maximum (U(z) horizontal velocity profile, ρ(z) density along the vertical z). Only unstable modes in waves of sufficient strength have the chance to grow sufficiently fast to develop breaking: the waves that broke had an estimated growth (of unstable modes) more than 3.3–3.7 times than in the strongest stable case. Evaluation of the minimum Richardson number (Rimin, in the pycnocline), the horizontal length of a pocket of possible instability, with wave-induced Ri < 14, (Lx) and the wavelength (λ), showed that all measurements fall within the range Rimin = −0.23Lx/λ + 0.298 ± 0.016 in the (Lx/λ, Rimin)-plane. Breaking ISWs were found for Lx/λ > 0.86 and stable waves for Lx/λ < 0.86. The results show a sort of threshold-like behaviour in terms of Lx/λ. The results demonstrate that the breaking threshold of Lx/λ = 0.86 was sharper than one based on a minimum Richardson number and reveal that the Richardson number was found to become almost antisymmetric across relatively thick pycnoclines, with the minimum occurring towards the top part of the pycnocline.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2009
References
REFERENCES
- 74
- Cited by

