Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T12:11:39.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Ship waves in the presence of uniform vorticity

Published online by Cambridge University Press:  21 February 2014

Simen Å. Ellingsen Open the ORCID record for Simen Å. Ellingsen [Opens in a new window]
Simen Å. Ellingsen*
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
*
†Email address for correspondence: simen.a.ellingsen@ntnu.no
Get access Rights & Permissions [Opens in a new window]

Abstract

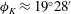Lord Kelvin’s result that waves behind a ship lie within a half-angle $\phi _{\mathit{K}}\approx 19^{\circ }28'$ is perhaps the most famous and striking result in the field of surface waves. We solve the linear ship wave problem in the presence of a shear current of constant vorticity 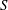$S$, and show that the Kelvin angles (one each side of wake) as well as other aspects of the wake depend closely on the ‘shear Froude number’ 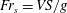$\mathit{Fr}_{\mathit{s}}=VS/g$ (based on length 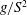$g/S^2$ and the ship’s speed 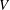$V$), and on the angle between current and the ship’s line of motion. In all directions except exactly along the shear flow there exists a critical value of 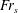$\mathit{Fr}_{\mathit{s}}$ beyond which no transverse waves are produced, and where the full wake angle reaches 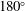$180^\circ $. Such critical behaviour is previously known from waves at finite depth. For side-on shear, one Kelvin angle can exceed 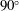$90^\circ $. On the other hand, the angle of maximum wave amplitude scales as 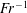$\mathit{Fr}^{-1}$ (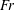$\mathit{Fr}$ based on size of ship) when 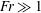$\mathit{Fr}\gg 1$, a scaling virtually unaffected by the shear flow.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Wakes/Jets: Wakes Waves/Free-surface Flows: Shear waves
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 742 , 10 March 2014 , R2
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bender, C. M. & Orszag, S. A. 1991 Advanced Mathematical Methods for Scientists and Engineers. Springer.Google Scholar
Benzaquen, M. & Raphaël, E. 2012 Capillary–gravity waves on depth-dependent currents: consequences for the wave resistance. EPL 97, 14007.Google Scholar
Booker, J. R. & Bretherton, F. P. 1967 The critical layer for internal gravity waves in a shear flow. J. Fluid Mech. 27, 513–539.Google Scholar
Brevik, I. 1976 The stopping of linear gravity waves in currents of uniform vorticity. Phys. Norvegica 8, 157–162.Google Scholar
Bühler, O. 2009 Waves and Mean Flow. Cambridge University Press.CrossRefGoogle Scholar
Darmon, A., Benzaquen, M. & Raphaël, E. 2014 Kelvin wake pattern at large Froude numbers. J. Fluid Mech. 738, R3.Google Scholar
Ellingsen, S.Å. & Brevik, I. 2014 How linear surface waves are affected by a current with constant vorticity. Eur. J. Phys. (accepted).CrossRefGoogle Scholar
Evans, J. T. 1955 Pneumatic and similar breakwaters. Proc. R. Soc. London A 231, 457–466.Google Scholar
Fabrikant, A. L. & Stepanyants, Y. A. 1998 Propagation of Waves in Shear Flows. World Scientific.Google Scholar
Faltinsen, O. M. 2005 Hydrodynamics of High-Speed Marine Vehicles. Cambridge University Press.Google Scholar
Havelock, T. H. 1908 The propagation of groups of waves in dispersive media, with application to waves on water produced by a travelling disturbance. Proc. R. Soc. London A 81, 398–430.Google Scholar
Havelock, T. H. 1919 Wave resistance: Some cases of three-dimensional fluid motion. Proc. R. Soc. London A 95, 354–365.Google Scholar
LeBlond, P. H. & Mysak, L. A. 1978 Waves in the Ocean. Elsevier.Google Scholar
McCue, S. W. & Forbes, L. K. 1999 Bow and stern flows with constant vorticity. J. Fluid Mech. 399, 277–300.Google Scholar
Peregrine, D. H. 1971 A ship’s waves and its wake. J. Fluid Mech. 49, 353–360.CrossRefGoogle Scholar
Peregrine, D. H. 1976 Interaction of water waves and currents. Adv. Appl. Mech. 16, 9–117.Google Scholar
Rabaud, M. & Moisy, F. 2013 Ship waves: Kelvin or Mach angle?. Phys. Rev. Lett. 110, 214503.Google Scholar
Raphaël, E. & de Gennes, P.-G. 1996 Capillary gravity waves caused by a moving disturbance: wave resistance. Phys. Rev. E 53, 3448–3455.Google Scholar
Reed, A. M. & Milgram, J. H. 2002 Ship wakes and their radar images. Annu. Rev. Fluid Mech. 34, 469–502.Google Scholar
Taylor, G. 1955 The action of a surface current used as a breakwater. Proc. R. Soc. London A 231, 466–478.Google Scholar
Teles da Silva, A. F. & Peregrine, D. H. 1988 Steep, steady surface waves on water of finite depth with constant vorticity. J. Fluid Mech. 195, 281–302.Google Scholar
Thomson (Lord Kelvin), W. 1887 On ship waves. Proc. Inst. Mech. Eng. 38, 409–434.Google Scholar
Wehausen, J. W. & Laitone, E. V. 1960 Surface waves. In Fluid Dynamics III (ed. Flügge, S.), Encyclopedia of Physics, vol. 9, pp. 446–778. Springer.Google Scholar