Hostname: page-component-857557d7f7-bvshn Total loading time: 0 Render date: 2025-11-20T08:28:33.698Z Has data issue: false hasContentIssue false
  • English
  • Français

Small-scale dynamo action in rotating compressible convection

Published online by Cambridge University Press:  21 November 2011

B. Favier  and
P. J. Bushby
B. Favier*
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
P. J. Bushby
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
*
†Email address for correspondence: benjamin.favier@ncl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study dynamo action in a convective layer of electrically conducting, compressible fluid, rotating about the vertical axis. At the upper and lower bounding surfaces, perfectly conducting boundary conditions are adopted for the magnetic field. Two different levels of thermal stratification are considered. If the magnetic diffusivity is sufficiently small, the convection acts as a small-scale dynamo. Using a definition for the magnetic Reynolds number 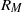that is based upon the horizontal integral scale and the horizontally averaged velocity at the mid-layer of the domain, we find that rotation tends to reduce the critical value of 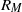above which dynamo action is observed. Increasing the level of thermal stratification within the layer does not significantly alter the critical value of 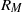in the rotating calculations, but it does lead to a reduction in this critical value in the non-rotating cases. At the highest computationally accessible values of the magnetic Reynolds number, the saturation levels of the dynamo are similar in all cases, with the mean magnetic energy density somewhere between 4 and 9 % of the mean kinetic energy density. To gain further insights into the differences between rotating and non-rotating convection, we quantify the stretching properties of each flow by measuring Lyapunov exponents. Away from the boundaries, the rate of stretching due to the flow is much less dependent upon depth in the rotating cases than it is in the corresponding non-rotating calculations. It is also shown that the effects of rotation significantly reduce the magnetic energy dissipation in the lower part of the layer. We also investigate certain aspects of the saturation mechanism of the dynamo.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory Geophysical and Geological Flows: Rotating flows

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 690 , 10 January 2012 , pp. 262 - 287
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1. Baliunas, S. L., Nesme-Ribes, E., Sokoloff, D. & Soon, W. H. 1996 A dynamo interpretation of stellar activity cycles. Astrophys. J. 460, 848–854.CrossRefGoogle Scholar
2. Brandenburg, A., Jennings, R. L., Nordlund, Å., Rieutord, M., Stein, R. F. & Tuominen, I. 1996 Magnetic structures in a dynamo simulation. J. Fluid Mech. 306, 325–352.CrossRefGoogle Scholar
3. Brandenburg, A., Klapper, I. & Kurths, J. 1995 Generalized entropies in a turbulent dynamo simulation. Phys. Rev. E 52, R4602–R4605.CrossRefGoogle Scholar
4. Brummell, N. H., Cattaneo, F. & Tobias, S. M. 1998a Linear and nonlinear dynamo action. Phys. Lett. A 249, 437–442.CrossRefGoogle Scholar
5. Brummell, N. H., Hurlburt, N. E. & Toomre, J. 1996 Turbulent compressible convection with rotation. Part I. Flow structure and evolution. Astrophys. J. 473, 494–513.CrossRefGoogle Scholar
6. Brummell, N. H., Hurlburt, N. E. & Toomre, J. 1998b Turbulent compressible convection with rotation. Part II. Mean flows and differential rotation. Astrophys. J. 493, 955–969.CrossRefGoogle Scholar
7. Brummell, N. H., Tobias, S. M. & Cattaneo, F. 2010 Dynamo efficiency in compressible convective dynamos with and without penetration. Geophys. Astrophys. Fluid Dyn. 104, 565–576.CrossRefGoogle Scholar
8. Brun, A. S., Miesch, M. S. & Toomre, J. 2004 Global-scale turbulent convection and magnetic dynamo action in the solar envelope. Astrophys. J. 614, 1073–1098.CrossRefGoogle Scholar
9. Bushby, P. J., Houghton, S. M., Proctor, M. R. E. & Weiss, N. O. 2008 Convective intensification of magnetic fields in the quiet sun. Mon. Not. R. Astron. Soc. 387, 698–706.CrossRefGoogle Scholar
10. Bushby, P. J., Proctor, M. R. E. & Weiss, N. O. 2010 Small-scale dynamo action in compressible convection. In Numerical Modelling of Space Plasma Flows, Astronum-2009 (ed. Pogorelov, N. V., Audit, E. & Zank, G. P. ). Astronomical Society of the Pacific Conference Series , vol. 429, pp. 181–186.Google Scholar
11. Cattaneo, F. 1999 On the origin of magnetic fields in the quiet photosphere. Astrophys. J. 515, L39–L42.CrossRefGoogle Scholar
12. Cattaneo, F. & Hughes, D. W. 2006 Dynamo action in a rotating convective layer. J. Fluid Mech. 553, 401–418.CrossRefGoogle Scholar
13. Cattaneo, F., Hughes, D. W. & Kim, E. 1996 Suppression of chaos in a simplified nonlinear dynamo model. Phys. Rev. Lett. 76, 2057–2060.CrossRefGoogle Scholar
14. Cattaneo, F. & Tobias, S. M. 2009 Dynamo properties of the turbulent velocity field of a saturated dynamo. J. Fluid Mech. 621, 205–214.CrossRefGoogle Scholar
15. Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
16. Childress, S. & Soward, A. M. 1972 Convection-driven hydromagnetic dynamo. Phys. Rev. Lett. 29, 837–839.CrossRefGoogle Scholar
17. Eckhardt, B. & Yao, D. 1993 Local Lyapunov exponents in chaotic systems. Physica D 65, 100–108.CrossRefGoogle Scholar
18. Favier, B. F. N., Godeferd, F. S. & Cambon, C. 2011 On the effect of rotation on MHD turbulence at high magnetic Reynolds number. Geophys. Astrophys. Fluid Dyn.Google Scholar
19. Finn, J. M. & Ott, E. 1988 Chaotic flows and fast magnetic dynamos. Phys. Fluids 31, 2992–3011.CrossRefGoogle Scholar
20. Gough, D. O., Moore, D. R., Spiegel, E. A. & Weiss, N. O. 1976 Convective instability in a compressible atmosphere. Part II. Astrophys. J. 206, 536–542.CrossRefGoogle Scholar
21. Haugen, N. E. L., Brandenburg, A. & Dobler, W. 2004 Simulations of nonhelical hydromagnetic turbulence. Phys. Rev. E 70, 016308.CrossRefGoogle ScholarPubMed
22. Hughes, D. W. & Proctor, M. R. E. 2009 Large-scale dynamo action driven by velocity shear and rotating convection. Phys. Rev. Lett. 102, 044501.CrossRefGoogle ScholarPubMed
23. Jones, C. A. & Roberts, P. H. 2000 Convection-driven dynamos in a rotating plane layer. J. Fluid Mech. 404, 311–343.CrossRefGoogle Scholar
24. Käpylä, P. J., Korpi, M. J. & Brandenburg, A. 2008 Large-scale dynamos in turbulent convection with shear. Astron. Astrophys. 491, 353–362.CrossRefGoogle Scholar
25. Käpylä, P. J., Korpi, M. J. & Brandenburg, A. 2009 Large-scale dynamos in rigidly rotating turbulent convection. Astrophys. J. 697, 1153–1163.CrossRefGoogle Scholar
26. Käpylä, P. J., Korpi, M. J. & Brandenburg, A. 2010 Open vs closed boundaries in large-scale convective dynamos. Astron. Astrophys. 518, A22.CrossRefGoogle Scholar
27. Matthews, P. C., Proctor, M. R. E. & Weiss, N. O. 1995 Compressible magnetoconvection in three dimensions: planforms and nonlinear behaviour. J. Fluid Mech. 305, 281–305.CrossRefGoogle Scholar
28. Meneguzzi, M. & Pouquet, A. 1989 Turbulent dynamos driven by convection. J. Fluid Mech. 205, 297–398.CrossRefGoogle Scholar
29. Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
30. Monchaux, R., Berhanu, M., Aumaître, S., Chiffaudel, A., Daviaud, F., Dubrulle, B., Ravelet, F., Fauve, S., Mordant, N., Pétrélis, F., Bourgoin, M., Odier, P., Pinton, J.-F., Plihon, N. & Volk, R. 2009 The von Kármán sodium experiment: turbulent dynamical dynamos. Phys. Fluids 21 (3), 035108.CrossRefGoogle Scholar
31. Roberts, P. H. & Glatzmaier, G. A. 2000 Geodynamo theory and simulations. Rev. Mod. Phys. 72, 1081–1123.CrossRefGoogle Scholar
32. Rogachevskii, I. & Kleeorin, N. 1997 Intermittency and anomalous scaling for magnetic fluctuations. Phys. Rev. E 56, 417–426.CrossRefGoogle Scholar
33. Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L. & McWilliams, J. C. 2004 Simulations of the small-scale turbulent dynamo. Astrophys. J. 612, 276–307.CrossRefGoogle Scholar
34. Servidio, S., Matthaeus, W. H. & Dmitruk, P. 2008 Depression of nonlinearity in decaying isotropic MHD turbulence. Phys. Rev. Lett. 100, 095005.CrossRefGoogle ScholarPubMed
35. St. Pierre, M. G. 1993 The strong field branch of the Childress–Soward dynamo. In Solar and Planetary Dynamos (ed. Proctor, M. R. E., Matthews, P. C. & Rucklidge, A. M. ). pp. 295–302.Google Scholar
36. Stellmach, S. & Hansen, U. 2004 Cartesian convection driven dynamos at low Ekman number. Phys. Rev. E 70, 056312.CrossRefGoogle ScholarPubMed
37. Stix, M. 2004 The Sun: An Introduction. Springer.Google Scholar
38. Tanner, S. E. M. & Hughes, D. W. 2003 Fast-dynamo action for a family of parametrized flows. Astrophys. J. 586, 685–691.CrossRefGoogle Scholar
39. Thelen, J.-C. & Cattaneo, F. 2000 Dynamo action driven by convection: the influence of magnetic boundary conditions. Mon. Not. R. Astron. Soc. 315, L13–L17.CrossRefGoogle Scholar
40. Vögler, A. & Schüssler, M. 2007 A solar surface dynamo. Astron. Astrophys. 465, L43–L46.CrossRefGoogle Scholar