Article contents
Sources and fluxes of scale energy in the overlap layer of wall turbulence
Published online by Cambridge University Press: 20 April 2015
Abstract
Direct numerical simulations of turbulent channel flows at friction Reynolds numbers (Re) of 550, 1000 and 1500 are used to analyse the turbulent production, transfer and dissipation mechanisms in the compound space of scales and wall distances by means of the Kolmogorov equation generalized to inhomogeneous anisotropic flows. Two distinct peaks of scale-energy source are identified. The first, stronger one, belongs to the near-wall cycle. Its location in the space of scales and physical space is found to scale in viscous units, while its intensity grows slowly with 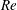 $\mathit{Re}$ , indicating a near-wall modulation. The second source peak is found further away from the wall in the putative overlap layer, and it is separated from the near-wall source by a layer of significant scale-energy sink. The dynamics of the second outer source appears to be strongly dependent on the Reynolds number. The detailed scale-by-scale analysis of this source highlights well-defined features that are used to make the properties of the outer turbulent source independent of Reynolds number and wall distance by rescaling the problem. Overall, the present results suggest a strong connection of the observed outer scale-energy source with the presence of an outer region of turbulence production whose mechanisms are well separated from the near-wall region and whose statistical features agree with the hypothesis of an overlap layer dominated by attached eddies. Inner–outer interactions between the near-wall and outer source region in terms of scale-energy fluxes are also analysed. It is conjectured that the near-wall modulation of the statistics at increasing Reynolds number can be related to a confinement of the near-wall turbulence production due to the presence of increasingly large production scales in the outer scale-energy source region.
$\mathit{Re}$ , indicating a near-wall modulation. The second source peak is found further away from the wall in the putative overlap layer, and it is separated from the near-wall source by a layer of significant scale-energy sink. The dynamics of the second outer source appears to be strongly dependent on the Reynolds number. The detailed scale-by-scale analysis of this source highlights well-defined features that are used to make the properties of the outer turbulent source independent of Reynolds number and wall distance by rescaling the problem. Overall, the present results suggest a strong connection of the observed outer scale-energy source with the presence of an outer region of turbulence production whose mechanisms are well separated from the near-wall region and whose statistical features agree with the hypothesis of an overlap layer dominated by attached eddies. Inner–outer interactions between the near-wall and outer source region in terms of scale-energy fluxes are also analysed. It is conjectured that the near-wall modulation of the statistics at increasing Reynolds number can be related to a confinement of the near-wall turbulence production due to the presence of increasingly large production scales in the outer scale-energy source region.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 29
- Cited by


