Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-26T02:06:11.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatial–spectral characteristics of momentum transport in a turbulent boundary layer

Published online by Cambridge University Press:  12 December 2017

D. Fiscaletti Open the ORCID record for D. Fiscaletti [Opens in a new window] ,
R. de Kat Open the ORCID record for R. de Kat [Opens in a new window]  and
B. Ganapathisubramani
D. Fiscaletti*
Affiliation:
Engineering and the Environment, University of Southampton, Highfield, Southampton SO17 1BJ, UK
R. de Kat
Affiliation:
Engineering and the Environment, University of Southampton, Highfield, Southampton SO17 1BJ, UK
B. Ganapathisubramani
Affiliation:
Engineering and the Environment, University of Southampton, Highfield, Southampton SO17 1BJ, UK
*
†Email address for correspondence: dan.fiscaletti@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Spectral content and spatial organization of momentum transport events are investigated in a turbulent boundary layer at the Reynolds number 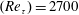$(Re_{\unicode[STIX]{x1D70F}})=2700$, with time-resolved planar particle image velocimetry. The spectral content of the Reynolds-shear-stress fluctuations reveals that the largest range of time and length scales can be observed in proximity to the wall, while this range becomes progressively more narrow when the wall distance increases. Farther from the wall, longer time and larger length scales exhibit an increasing spectral content. Wave velocities of transport events are estimated from wavenumber–frequency power spectra at different wall-normal locations. Wave velocities associated with ejection events (Q2) are lower than the local average streamwise velocity, while sweep events (Q4) are characterized by wave velocities larger than the local average velocity. These velocity deficits are almost insensitive to the wall distance, which is also confirmed from time tracking the intense transport events. The vertical advection velocities of the intense ejection and sweep events are on average a small fraction of the friction velocity 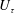$U_{\unicode[STIX]{x1D70F}}$, different from previous observations in a channel flow. In the range of wall-normal locations 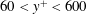$60<y^{+}<600$, sweeps are considerably larger than ejections, which could be because the ejections are preferentially located in between the legs of hairpin packets. Finally, it is observed that negative quadrant events of the same type tend to appear in groups over a large spatial streamwise extent.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 836 , 10 February 2018 , pp. 599 - 634
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Antonia, R. A., Teitel, M., Kim, J. & Browne, L. W. B. 1992 Low-Reynolds-number effects in a fully developed turbulent channel flow. J. Fluid Mech. 236, 579–605.Google Scholar
Bernard, P. S. & Wallace, J. M. 2002 Turbulent Flow: Analysis, Measurement, and Prediction. Wiley.Google Scholar
Blackwelder, R. F. & Kaplan, R. E. 1976 On the wall structure of the turbulent boundary layer. J. Fluid Mech. 76, 89–112.Google Scholar
Bogard, D. G. & Tiederman, W. G. 1986 Burst detection with single-point velocity measurements. J. Fluid Mech. 162, 389–413.Google Scholar
Bogard, D. G., Wallace, J. M. & Eckelmann, H. 1974 Some properties of truncated turbulence signals in bounded shear flows. J. Fluid Mech. 63, 209–224.Google Scholar
Dong, S., Lozano-Durán, A., Sekimoto, A. & Jiménez, J. 2017 Coherent structures in statistically stationary homogeneous shear turbulence. J. Fluid Mech. 816, 167–208.Google Scholar
Elsinga, G. E., Adrian, R. J., van Oudheusden, B. W. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
Flores, O., Jiménez, J. & del Álamo, J. C. 2007 Vorticity organization in the outer layer of turbulent channels with disturbed walls. J. Fluid Mech. 591, 145–154.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Gander, W., Golub, G. H. & Strebel, R. 1994 Least-squares fitting of circles and ellipses. BIT Numer. Maths 34, 558–578.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Herpin, S., Stanislas, M. & Soria, J. 2010 The organization of near-wall turbulence: a comparison between boundary layer SPIV data and channel flow DNS data. J. Turbul. 47, 1–30.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Jodai, Y. & Elsinga, G. E. 2016 Experimental observation of hairpin auto-generation events in a turbulent boundary layer. J. Fluid Mech. 795, 611–633.CrossRefGoogle Scholar
de Kat, R. & Ganapathisubramani, B. 2015a Convection of momentum transport events in a turbulent boundary layer. In 9th International Symposium on Turbulence and Shear Flow Phenomena (TSFP-9), 30 June–3 July, Melbourne, Australia.Google Scholar
de Kat, R. & Ganapathisubramani, B. 2015b Frequency-wavenumber mapping in turbulent shear flows. J. Fluid Mech. 783, 166–190.Google Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
LeHew, J., Guala, M. & McKeon, B. 2013 Time-resolved measurements of coherent structures in the turbulent boundary layer. Exp. Fluids 4, 1–16.Google Scholar
Lin, C.-L., McWilliams, J. C., Moeng, C.-H. & Sullivan, P. P. 1996 Coherent structures and dynamics in a neutrally stratified planetary boundary layer flow. Phys. Fluids 8, 2626–2639.Google Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.Google Scholar
Lu, S. S. & Willmarth, W. W. 1973 Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–511.Google Scholar
Morrill-Winter, C., Philip, J. & Klewicki, J. 2017 Statistical evidence of an asymptotic geometric structure to the momentum transporting motions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 375, 1–14.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11, 943–945.Google Scholar
Nagano, Y. & Tagawa, M. 1998 Statistical characteristics of wall turbulence with a passive scalar. J. Fluid Mech. 196, 157–185.Google Scholar
Nakagawa, H. & Nezu, I. 1977 Prediction of the contributions to the Reynolds stress from bursting events in open-channel flows. J. Fluid Mech. 80, 99–128.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Priyadarshana, P. J. A. & Klewicki, J. C. 2004 Study of the motions contributing to the Reynolds stress in high and low Reynolds number turbulent boundary layers. Phys. Fluids 16, 4586–4600.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Strickland, J. H. & Simpson, R. L. 1975 ‘Bursting’ frequencies obtained from wall shear stress fluctuations in a turbulent boundary layer. Phys. Fluids 18, 306–308.Google Scholar
Tanahashi, M., Kang, S. J., Miyamoto, T., Shiokawa, S. & Miyauchi, T. 2004 Scaling law of fine scale eddies in turbulent channel flows up to Re 𝜏 = 800. Intl J. Heat Fluid Flow 25, 331–340.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11, 97–120.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48, 131–158.Google Scholar
Wallace, J. M., Eckelman, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.CrossRefGoogle Scholar
Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55, 65–92.Google Scholar
Zhou, J., Adrian, R. J. & Balachandar, S. 1996 Autogeneration of near-wall vortical structures in channel flow. Phys. Fluids 8, 288–290.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar

Fiscaletti et al. supplementary movie 1

Time evolution of negative and positive quadrant events of the Reynolds shear stresses. Black dashed lines mark intense Q+ events, while black continuous lines mark intense Q-events. Spots of different sizes and shades mark the time evolution of the weighted centroids of the intense events. The time span covered in this video is 1.33δ/U∞.

Download Fiscaletti et al. supplementary movie 1(Video)
Video 26.7 MB

Fiscaletti et al. supplementary movie 2

Time evolution of ejection (red) and sweep (blue) events. Black continuous lines mark intense ejection events, while black dashed lines mark intense sweep events. Spots of different sizes and shades mark the time evolution of the weighted centroids of the intense events. The time span covered in this video is 1.33δ/U∞.

Download Fiscaletti et al. supplementary movie 2(Video)
Video 20.6 MB