Hostname: page-component-5db58dd55d-m58mf Total loading time: 0 Render date: 2026-06-16T19:02:49.736Z Has data issue: false hasContentIssue false
  • English
  • Français

Spike formation theory in three-dimensional flow separation

Published online by Cambridge University Press:  22 August 2023

Sreejith Santhosh ,
Haodong Qin ,
Bjoern F. Klose ,
Gustaaf B. Jacobs Open the ORCID record for Gustaaf B. Jacobs [Opens in a new window] ,
Jérôme Vétel Open the ORCID record for Jérôme Vétel [Opens in a new window]  and
Mattia Serra Open the ORCID record for Mattia Serra [Opens in a new window]
Sreejith Santhosh
Affiliation:
Department of Physics, University of California, San Diego, CA 92093, USA
Haodong Qin
Affiliation:
Department of Physics, University of California, San Diego, CA 92093, USA
Bjoern F. Klose
Affiliation:
Department of Aerospace Engineering, San Diego State University, San Diego, CA 92182, USA Institute of Test and Simulation for Gas Turbines, German Aerospace Center (DLR), 86159 Augsburg, Germany
Gustaaf B. Jacobs
Affiliation:
Department of Aerospace Engineering, San Diego State University, San Diego, CA 92182, USA
Jérôme Vétel
Affiliation:
Department of Mechanical Engineering, Polytechnique Montréal, Montréal, QC H3C 3A7, Canada
Mattia Serra*
Affiliation:
Department of Physics, University of California, San Diego, CA 92093, USA
*
†Email address for correspondence: mserra@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

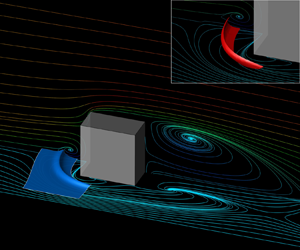
We develop a frame-invariant theory of material spike formation during flow separation over a no-slip boundary in three-dimensional flows with arbitrary time dependence. Based on the exact evolution of the largest principal curvature on near-wall material surfaces, our theory identifies fixed and moving separation. Our approach is effective over short time intervals and admits an instantaneous limit. As a byproduct, we derive explicit formulas for the evolution of the Weingarten map and the principal curvatures of any surface advected by general three-dimensional flows. The material backbone we identify acts first as a precursor and later as the centrepiece of Lagrangian flow separation. We discover previously undetected spiking points and curves where the separation backbones connect to the boundary and provide wall-based analytical formulas for their locations. We illustrate our results on several steady and unsteady flows.

JFM classification

Boundary Layers: Boundary layer separation Nonlinear Dynamical Systems: Pattern formation Wakes/Jets: Separated flows

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 969 , 25 August 2023 , A25
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alam, M. & Sandham, N.D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 410, 1–28.CrossRefGoogle Scholar
Bhattacharjee, D., Klose, B., Jacobs, G.B. & Hemati, M.S. 2020 Data-driven selection of actuators for optimal control of airfoil separation. Theor. Comput. Fluid Dyn. 34 (4), 557–575.CrossRefGoogle Scholar
Cattafesta, L.N. & Sheplak, M. 2011 Actuators for active flow control. Annu. Rev. Fluid Mech. 43, 247–272.CrossRefGoogle Scholar
Délery, J.M. 2001 Robert legendre and henri werlé: toward the elucidation of three-dimensional separation. Annu. Rev. Fluid Mech. 33, 129–154.CrossRefGoogle Scholar
Deparday, J., He, X., Eldredge, J.D., Mulleners, K. & Williams, D.R. 2022 Experimental quantification of unsteady leading-edge flow separation. J. Fluid Mech. 941, A60.CrossRefGoogle Scholar
Gautier, R., Laizet, S. & Lamballais, E. 2014 A DNS study of jet control with microjets using an immersed boundary method. Intl J. Comput. Fluid Dyn. 28 (6–10), 393–410.CrossRefGoogle Scholar
Green, M.A., Rowley, C.W. & Haller, G. 2007 Detection of lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 572, 111–120.CrossRefGoogle Scholar
Greenblatt, D. & Wygnanski, I.J. 2000 The control of flow separation by periodic excitation. Prog. Aerosp. Sci. 36 (7), 487–545.CrossRefGoogle Scholar
Haller, G. 2004 Exact theory of unsteady separation for two-dimensional flows. J. Fluid Mech. 512, 257–311.CrossRefGoogle Scholar
Haller, G. 2015 Lagrangian coherent structures. Annu. Rev. Fluid Mech. 47, 137–162.CrossRefGoogle Scholar
Hemati, M.S., Deem, E.A., Williams, M.O., Rowley, C.W. & Cattafesta, L.N. 2016 Improving separation control with noise-robust variants of dynamic mode decomposition. In 54th AIAA Aerospace Sciences Meeting, p.1103. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Jacobs, G.B., Surana, A., Peacock, T. & Haller, G. 2007 Identification of flow separation in three and four dimensions. In 45th AIAA Aerospace Sciences Meeting and Exhibit, p. 401. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Kamphuis, M., Jacobs, G.B., Chen, K., Spedding, G. & Hoeijmakers, H. 2018 Pulse actuation and its effects on separated lagrangian coherent structures for flow over acambered airfoil. In 2018 AIAA Aerospace Sciences Meeting, p. 2255. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Klonowska-Prosnak, M.E. & Prosnak, W.J. 2001 An exact solution to the problem of creeping flow around circular cylinder rotating in presence of translating plane boundary. Acta Mech. 146 (1), 115–126.CrossRefGoogle Scholar
Klose, B.F., Jacobs, G.B. & Kopriva, D.A. 2020 a Assessing standard and kinetic energy conserving volume fluxes in discontinuous galerkin formulations for marginally resolved Navier-Stokes flows. Comput. Fluids 205, 104557.CrossRefGoogle Scholar
Klose, B.F., Serra, M. & Jacobs, G.B. 2020 b Kinematics of Lagrangian flow separation in external aerodynamics. AIAA J. 58 (5), 1926–1938.CrossRefGoogle Scholar
Kopriva, D.A. 2009 Implementing Spectral Methods for Partial Differential Equations. Springer.CrossRefGoogle Scholar
Kuhnel, W. & Hunt, B. 2015 Differential Geometry: Curves, Surfaces, Manifolds, vol. 160. Springer Science & Business Media.CrossRefGoogle Scholar
Laizet, S. & Lamballais, E. 2009 High-order compact schemes for incompressible flows: a simple and efficient method with quasi-spectral accuracy. J. Comput. Phys. 228 (16), 5989–6015.CrossRefGoogle Scholar
Laizet, S. & Li, N. 2011 Incompact3d: a powerful tool to tackle turbulence problems with up to $O(10^5)$ computational cores. Intl J. Numer. Meth. Fluids 67, 1735–1757.CrossRefGoogle Scholar
Le Fouest, S., Deparday, J. & Mulleners, K. 2021 The dynamics and timescales of static stall. J. Fluids Struct. 104, 103304.CrossRefGoogle Scholar
Legendre, R. 1956 Séparation de l’écoulement laminaire tridimensionnel. Rech. Aérosp. 54 (54), 3–8.Google Scholar
Lighthill, M.J. 1963 Boundary layer theory. In Laminar Boundary Layers, pp. 46–113. Oxford University Press.Google Scholar
Liu, C.S. & Wan, Y.-H. 1985 A simple exact solution of the Prandtl boundary layer equations containing a point of separation. Arch. Rat. Mech. Anal. 89 (2), 177–185.CrossRefGoogle Scholar
Melius, M., Cal, R.B. & Mulleners, K. 2016 Dynamic stall of an experimental wind turbine blade. Phys. Fluids 28 (3), 034103.CrossRefGoogle Scholar
Melius, M.S., Mulleners, K. & Cal, R.B. 2018 The role of surface vorticity during unsteady separation. Phys. Fluids 30 (4), 045108.CrossRefGoogle Scholar
Miron, P. & Vétel, J. 2015 Towards the detection of moving separation in unsteady flows. J. Fluid Mech. 779, 819–841.CrossRefGoogle Scholar
Prandtl, L. 1904 Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Des Dritten Internationalen Mathematiker-Kongresses Heidelberg. Leipzig.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory, 8th edn. Springer.CrossRefGoogle Scholar
Sears, W.R. & Telionis, D.P. 1971 Unsteady boundary-layer separation. In Recent Research on Unsteady Boundary Layers, vol. 1, pp. 404–447. Laval University Press.Google Scholar
Sears, W.R. & Telionis, D.P. 1975 Boundary-layer separation in unsteady flow. SIAM J. Appl. Maths 28 (1), 215–235.CrossRefGoogle Scholar
Serra, M., Crouzat, S., Simon, G., Vétel, J. & Haller, G. 2020 Material spike formation in highly unsteady separated flows. J. Fluid Mech. 883, A30.CrossRefGoogle Scholar
Serra, M. & Haller, G. 2016 Objective Eulerian coherent structures. Chaos 26 (5), 053110.CrossRefGoogle ScholarPubMed
Serra, M., Vétel, J. & Haller, G. 2018 Exact theory of material spike formation in flow separation. J. Fluid Mech. 845, 51–92.CrossRefGoogle Scholar
Simpson, R.L. 1996 Aspects of turbulent boundary-layer separation. Prog. Aerosp. Sci. 32 (5), 457–521.CrossRefGoogle Scholar
Sudharsan, S., Ganapathysubramanian, B. & Sharma, A. 2022 A vorticity-based criterion to characterise leading edge dynamic stall onset. J. Fluid Mech. 935, A10.CrossRefGoogle Scholar
Surana, A., Grunberg, O. & Haller, G. 2006 Exact theory of three-dimensional flow separation. Part 1. Steady separation. J. Fluid Mech. 564, 57–103.CrossRefGoogle Scholar
Surana, A., Jacobs, G.B., Grunberg, O. & Haller, G. 2008 An exact theory of three-dimensional fixed separation in unsteady flows. Phys. Fluids 20 (10), 107101.CrossRefGoogle Scholar
Surana, A., Jacobs, G.B. & Haller, G. 2007 Extraction of separation and attachment surfaces from three-dimensional steady shear flows. AIAA J. 45 (6), 1290–1302.CrossRefGoogle Scholar
Taira, K., Brunton, S.L., Dawson, S.T.M., Rowley, C.W., Colonius, T., McKeon, B.J., Schmidt, O.T., Gordeyev, S., Theofilis, V. & Ukeiley, L.S. 2017 Modal analysis of fluid flows: an overview. AIAA J. 55 (12), 4013–4041.CrossRefGoogle Scholar
Truesdell, C. & Noll, W. 2004 The Non-Linear Field Theories of Mechanics. Springer.CrossRefGoogle Scholar
Tobak, M. & Peake, D.J. 1982 Topology of three-dimensional separated flows. Annu. Rev. Fluid Mech. 14, 61–85.CrossRefGoogle Scholar
Wilson, Z.D., Tutkun, M. & Cal, R.B. 2013 Identification of lagrangian coherent structures in a turbulent boundary layer. J. Fluid Mech. 728, 396–416.CrossRefGoogle Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2015 Flow Separation and Separated Flows. Springer.CrossRefGoogle Scholar
Wu, J.Z., Tramel, R.W., Zhu, F.L. & Yin, X.Y. 2000 A vorticity dynamics theory of three-dimensional flow separation. Phys. Fluids 12 (8), 1932–1954.CrossRefGoogle Scholar
Yeh, C.-A. & Taira, K. 2019 Resolvent-analysis-based design of airfoil separation control. J. Fluid Mech. 867, 572–610.CrossRefGoogle Scholar
You, D. & Moin, P. 2008 Active control of flow separation over an airfoil using synthetic jets. J. Fluids Struct. 24 (8), 1349–1357.CrossRefGoogle Scholar

Santhosh et al. Supplementary Movie 1

Caption included in Figure 1

Download Santhosh et al. Supplementary Movie 1(Video)
Video 730 KB

Santhosh et al. Supplementary Movie 2

Caption included in Figure 3

Download Santhosh et al. Supplementary Movie 2(Video)
Video 363.7 KB

Santhosh et al. Supplementary Movie 3

Caption included in Figure 4

Download Santhosh et al. Supplementary Movie 3(Video)
Video 729.8 KB

Santhosh et al. Supplementary Movie 4

Caption included in Figure 5

Download Santhosh et al. Supplementary Movie 4(Video)
Video 293.3 KB

Santhosh et al. Supplementary Movie 5

Caption included in Figure 7

Download Santhosh et al. Supplementary Movie 5(Video)
Video 147 KB

Santhosh et al. Supplementary Movie 6

Caption included in Figure 7

Download Santhosh et al. Supplementary Movie 6(Video)
Video 180.2 KB

Santhosh et al. Supplementary Movie 7

Caption included in Figure 9

Download Santhosh et al. Supplementary Movie 7(Video)
Video 183.1 KB

Santhosh et al. Supplementary Movie 8

Caption included in Figure 11

Download Santhosh et al. Supplementary Movie 8(Video)
Video 191.4 KB

Santhosh et al. Supplementary Movie 9

Caption included in Figure 12

Download Santhosh et al. Supplementary Movie 9(Video)
Video 153.1 KB

Santhosh et al. Supplementary Movie 10

Caption included in Figure 12

Download Santhosh et al. Supplementary Movie 10(Video)
Video 150.1 KB