Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gordillo, José Manuel
and
Riboux, Guillaume
2019.
A note on the aerodynamic splashing of droplets.
Journal of Fluid Mechanics,
Vol. 871,
Issue. ,
Gordillo, José Manuel
Riboux, Guillaume
and
Quintero, Enrique S.
2019.
A theory on the spreading of impacting droplets.
Journal of Fluid Mechanics,
Vol. 866,
Issue. ,
p.
298.
Burzynski, David A.
Roisman, Ilia V.
and
Bansmer, Stephan E.
2020.
On the splashing of high-speed drops impacting a dry surface.
Journal of Fluid Mechanics,
Vol. 892,
Issue. ,
Wang, Fujun
and
Fang, Tiegang
2020.
Retraction dynamics of water droplets after impacting upon solid surfaces from hydrophilic to superhydrophobic.
Physical Review Fluids,
Vol. 5,
Issue. 3,
Kim, Seungho
Wu, Zixuan
Esmaili, Ehsan
Dombroskie, Jason J.
and
Jung, Sunghwan
2020.
How a raindrop gets shattered on biological surfaces.
Proceedings of the National Academy of Sciences,
Vol. 117,
Issue. 25,
p.
13901.
Naveen, P. T.
Simhadri, R. R.
and
Ranjith, S. K.
2020.
Simultaneous Effect of Droplet Temperature and Surface Wettability on Single Drop Impact Dynamics.
Fluid Dynamics,
Vol. 55,
Issue. 5,
p.
640.
Qin, Mengxiao
Tang, Chenglong
Guo, Yang
Zhang, Peng
and
Huang, Zuohua
2020.
Subpatterns of Thin-Sheet Splash on a Smooth Surface.
Langmuir,
Vol. 36,
Issue. 18,
p.
4917.
Hao, Jiguang
Lu, Jie
Zhang, Zihao
Wu, Zhihu
Hu, Gengkai
and
Floryan, J. M.
2020.
Asymmetric droplet splashing.
Physical Review Fluids,
Vol. 5,
Issue. 7,
Zhang, Haixiang
Zhang, Xiwen
Yi, Xian
He, Feng
Niu, Fenglei
and
Hao, Pengfei
2020.
Dynamic behaviors of droplets impacting on ultrasonically vibrating surfaces.
Experimental Thermal and Fluid Science,
Vol. 112,
Issue. ,
p.
110019.
Zhang, Haixiang
Zhang, Xiwen
Yi, Xian
He, Feng
Niu, Fenglei
and
Hao, Pengfei
2020.
Asymmetric splash and breakup of drops impacting on cylindrical superhydrophobic surfaces.
Physics of Fluids,
Vol. 32,
Issue. 12,
Liu, Chunbao
Liu, Qi
and
Lin, Zhaohua
2020.
Dynamical behavior of droplets transiently impacting on superhydrophobic microstructures.
Physics of Fluids,
Vol. 32,
Issue. 10,
García-Geijo, Paula
Riboux, Guillaume
and
Gordillo, José Manuel
2020.
Inclined impact of drops.
Journal of Fluid Mechanics,
Vol. 897,
Issue. ,
Zhang, Haixiang
Zhang, Xiwen
Yi, Xian
He, Feng
Niu, Fenglei
and
Hao, Pengfei
2021.
Effect of wettability on droplet impact: Spreading and splashing.
Experimental Thermal and Fluid Science,
Vol. 124,
Issue. ,
p.
110369.
Thoraval, Marie-Jean
Schubert, Jonas
Karpitschka, Stefan
Chanana, Munish
Boyer, François
Sandoval-Naval, Enrique
Dijksman, J. Frits
Snoeijer, Jacco H.
and
Lohse, Detlef
2021.
Nanoscopic interactions of colloidal particles can suppress millimetre drop splashing.
Soft Matter,
Vol. 17,
Issue. 20,
p.
5116.
Usawa, Masashi
Fujita, Yuta
Tagawa, Yoshiyuki
Riboux, Guillaume
and
Gordillo, José Manuel
2021.
Large impact velocities suppress the splashing of micron-sized droplets.
Physical Review Fluids,
Vol. 6,
Issue. 2,
García-Geijo, P.
Quintero, E. S.
Riboux, G.
and
Gordillo, J. M.
2021.
Spreading and splashing of drops impacting rough substrates.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Wei, Yu
and
Thoraval, Marie-Jean
2021.
Maximum spreading of an impacting air-in-liquid compound drop.
Physics of Fluids,
Vol. 33,
Issue. 6,
Quetzeri-Santiago, M. A.
Castrejón-Pita, J. R.
and
Castrejón-Pita, A. A.
2021.
Controlling droplet splashing and bouncing by dielectrowetting.
Scientific Reports,
Vol. 11,
Issue. 1,
Zhou, Shan
Jiang, Lei
and
Dong, Zhichao
2021.
Bioinspired Surface with Superwettability for Controllable Liquid Dynamics.
Advanced Materials Interfaces,
Vol. 8,
Issue. 2,
Qin, Yanzhou
Guo, Qiaoyu
Chen, Rouxian
Zhuang, Yuan
and
Wang, Yulin
2021.
Numerical investigation of water droplet impact on PEM fuel cell flow channel surface.
Renewable Energy,
Vol. 168,
Issue. ,
p.
750.
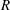 $R$ of a liquid of density
$R$ of a liquid of density 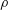 $\unicode[STIX]{x1D70C}$, viscosity
$\unicode[STIX]{x1D70C}$, viscosity 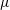 $\unicode[STIX]{x1D707}$ and interfacial tension coefficient
$\unicode[STIX]{x1D707}$ and interfacial tension coefficient  $\unicode[STIX]{x1D70E}$ impacting a superhydrophobic substrate at a velocity
$\unicode[STIX]{x1D70E}$ impacting a superhydrophobic substrate at a velocity 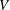 $V$ keeps its integrity and spreads over the solid for
$V$ keeps its integrity and spreads over the solid for 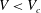 $V<V_{c}$ or splashes, disintegrating into tiny droplets violently ejected radially outwards for
$V<V_{c}$ or splashes, disintegrating into tiny droplets violently ejected radially outwards for 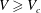 $V\geqslant V_{c}$, with
$V\geqslant V_{c}$, with 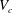 $V_{c}$ the critical velocity for splashing. In contrast with the case of drop impact onto a partially wetting substrate, Riboux & Gordillo (Phys. Rev. Lett., vol. 113, 2014, 024507), our experiments reveal that the critical condition for the splashing of water droplets impacting a superhydrophobic substrate at normal atmospheric conditions is characterized by a value of the critical Weber number,
$V_{c}$ the critical velocity for splashing. In contrast with the case of drop impact onto a partially wetting substrate, Riboux & Gordillo (Phys. Rev. Lett., vol. 113, 2014, 024507), our experiments reveal that the critical condition for the splashing of water droplets impacting a superhydrophobic substrate at normal atmospheric conditions is characterized by a value of the critical Weber number, 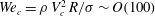 $We_{c}=\unicode[STIX]{x1D70C}\,V_{c}^{2}\,R/\unicode[STIX]{x1D70E}\sim O(100)$, which hardly depends on the Ohnesorge number
$We_{c}=\unicode[STIX]{x1D70C}\,V_{c}^{2}\,R/\unicode[STIX]{x1D70E}\sim O(100)$, which hardly depends on the Ohnesorge number 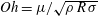 $Oh=\unicode[STIX]{x1D707}/\sqrt{\unicode[STIX]{x1D70C}\,R\,\unicode[STIX]{x1D70E}}$ and is noticeably smaller than the corresponding value for the case of partially wetting substrates. Here we present a self-consistent model, in very good agreement with experiments, capable of predicting
$Oh=\unicode[STIX]{x1D707}/\sqrt{\unicode[STIX]{x1D70C}\,R\,\unicode[STIX]{x1D70E}}$ and is noticeably smaller than the corresponding value for the case of partially wetting substrates. Here we present a self-consistent model, in very good agreement with experiments, capable of predicting 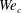 $We_{c}$ as well as the full dynamics of the drop expansion and disintegration for
$We_{c}$ as well as the full dynamics of the drop expansion and disintegration for 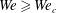 $We\geqslant We_{c}$. In particular, our model is able to accurately predict the time evolution of the position of the rim bordering the expanding lamella for
$We\geqslant We_{c}$. In particular, our model is able to accurately predict the time evolution of the position of the rim bordering the expanding lamella for 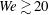 $We\gtrsim 20$ as well as the diameters and velocities of the small and fast droplets ejected when
$We\gtrsim 20$ as well as the diameters and velocities of the small and fast droplets ejected when 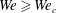 $We\geqslant We_{c}$.
$We\geqslant We_{c}$.
