Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gustavsson, K
Meneguz, E
Reeks, M
and
Mehlig, B
2012.
Inertial-particle dynamics in turbulent flows: caustics, concentration fluctuations and random uncorrelated motion.
New Journal of Physics,
Vol. 14,
Issue. 11,
p.
115017.
Karnik, Aditya U.
and
Shrimpton, John S.
2012.
Mitigation of preferential concentration of small inertial particles in stationary isotropic turbulence using electrical and gravitational body forces.
Physics of Fluids,
Vol. 24,
Issue. 7,
Devenish, B. J.
Bartello, P.
Brenguier, J.‐L.
Collins, L. R.
Grabowski, W. W.
IJzermans, R. H. A.
Malinowski, S. P.
Reeks, M. W.
Vassilicos, J. C.
Wang, L.‐P.
and
Warhaft, Z.
2012.
Droplet growth in warm turbulent clouds.
Quarterly Journal of the Royal Meteorological Society,
Vol. 138,
Issue. 667,
p.
1401.
Nott, P. R.
Davis, R. H.
Reeks, M.
Saintillan, D.
and
Sundaresan, S.
2013.
Report on the IUTAM Symposium on Mobile Particulate Systems: Kinematics, Rheology, and Complex Phenomena, Bangalore, India, 2012.
Physics of Fluids,
Vol. 25,
Issue. 7,
Bewley, Gregory P
Saw, Ewe-Wei
and
Bodenschatz, Eberhard
2013.
Observation of the sling effect.
New Journal of Physics,
Vol. 15,
Issue. 8,
p.
083051.
Dejoan, A.
and
Monchaux, R.
2013.
Preferential concentration and settling of heavy particles in homogeneous turbulence.
Physics of Fluids,
Vol. 25,
Issue. 1,
Nicolai, Claudia
Jacob, Boris
Gualtieri, Paolo
and
Piva, Renzo
2014.
Inertial Particles in Homogeneous Shear Turbulence: Experiments and Direct Numerical Simulation.
Flow, Turbulence and Combustion,
Vol. 92,
Issue. 1-2,
p.
65.
Masi, Enrica
and
Simonin, Olivier
2014.
Algebraic-Closure-Based Moment Method for Unsteady Eulerian Simulations of Non-Isothermal Particle-Laden Turbulent Flows at Moderate Stokes Numbers in Dilute Regime.
Flow, Turbulence and Combustion,
Vol. 92,
Issue. 1-2,
p.
121.
Ni, Rui
Ouellette, Nicholas T.
and
Voth, Greg A.
2014.
Alignment of vorticity and rods with Lagrangian fluid stretching in turbulence.
Journal of Fluid Mechanics,
Vol. 743,
Issue. ,
Reeks, Michael W
2014.
Transport, mixing and agglomeration of particles in turbulent flows.
Journal of Physics: Conference Series,
Vol. 530,
Issue. ,
p.
012003.
Bragg, Andrew D
and
Collins, Lance R
2014.
New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distribution of particles.
New Journal of Physics,
Vol. 16,
Issue. 5,
p.
055013.
Voßkuhle, Michel
Pumir, Alain
Lévêque, Emmanuel
and
Wilkinson, Michael
2014.
Prevalence of the sling effect for enhancing collision rates in turbulent suspensions.
Journal of Fluid Mechanics,
Vol. 749,
Issue. ,
p.
841.
Masi, E.
Simonin, O.
Riber, E.
Sierra, P.
and
Gicquel, L.Y.M.
2014.
Development of an algebraic-closure-based moment method for unsteady Eulerian simulations of particle-laden turbulent flows in very dilute regime.
International Journal of Multiphase Flow,
Vol. 58,
Issue. ,
p.
257.
Gustavsson, K.
Vajedi, S.
and
Mehlig, B.
2014.
Clustering of Particles Falling in a Turbulent Flow.
Physical Review Letters,
Vol. 112,
Issue. 21,
Reeks, Michael W
2014.
Transport, Mixing and Agglomeration of Particles in Turbulent Flows.
Flow, Turbulence and Combustion,
Vol. 92,
Issue. 1-2,
p.
3.
Gualtieri, P.
Picano, F.
Sardina, G.
and
Casciola, C. M.
2015.
Exact regularized point particle method for multiphase flows in the two-way coupling regime.
Journal of Fluid Mechanics,
Vol. 773,
Issue. ,
p.
520.
Farhan, M.
Nicolleau, F. C. G. A.
and
Nowakowski, A. F.
2015.
Effect of gravity on clustering patterns and inertial particle attractors in kinematic simulations.
Physical Review E,
Vol. 91,
Issue. 4,
Esmaily-Moghadam, Mahdi
and
Mani, Ali
2016.
Analysis of the clustering of inertial particles in turbulent flows.
Physical Review Fluids,
Vol. 1,
Issue. 8,
Lappa, Marcello
2016.
On the nature, formation and diversity of particulate coherent structures in microgravity conditions and their relevance to materials science and problems of astrophysical interest.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 110,
Issue. 4,
p.
348.
Gustavsson, K.
and
Mehlig, B.
2016.
Statistical models for spatial patterns of heavy particles in turbulence.
Advances in Physics,
Vol. 65,
Issue. 1,
p.
1.
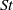 above which the net compressibility of the particle concentration changes sign (from compression to dilation). A further KS analysis is carried out by examining the distribution in time of the compression of an elemental volume of particles, which shows that it is close to Gaussian as far as the third and fourth moments but non-Gaussian (within the uncertainties of the measurements) for higher-order moments when the contribution of singularities in the tails of the distribution increasingly dominates the statistics. Measurements of the rate of occurrence of singularities show that it reaches a maximum at
above which the net compressibility of the particle concentration changes sign (from compression to dilation). A further KS analysis is carried out by examining the distribution in time of the compression of an elemental volume of particles, which shows that it is close to Gaussian as far as the third and fourth moments but non-Gaussian (within the uncertainties of the measurements) for higher-order moments when the contribution of singularities in the tails of the distribution increasingly dominates the statistics. Measurements of the rate of occurrence of singularities show that it reaches a maximum at 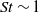 , with the distribution of times between singularities following a Poisson process. Following the approach used by Fevrier, Simonin & Squires (J. Fluid Mech., vol. 553, 2005, pp. 1–46), we also measured the random uncorrelated motion (RUM) and mesoscopic components of the compression for
, with the distribution of times between singularities following a Poisson process. Following the approach used by Fevrier, Simonin & Squires (J. Fluid Mech., vol. 553, 2005, pp. 1–46), we also measured the random uncorrelated motion (RUM) and mesoscopic components of the compression for 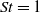 and show that the non-Gaussian highly intermittent part of the distribution of the compression is associated with the RUM component and ultimately with the occurrence of singularities. This result is consistent with the formation of caustics (Wilkinson et al. Phys. Fluids, vol. 19, 2007, p. 113303), where the activation of singularities precedes the crossing of trajectories (RUM).
and show that the non-Gaussian highly intermittent part of the distribution of the compression is associated with the RUM component and ultimately with the occurrence of singularities. This result is consistent with the formation of caustics (Wilkinson et al. Phys. Fluids, vol. 19, 2007, p. 113303), where the activation of singularities precedes the crossing of trajectories (RUM).
