Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T21:13:14.727Z Has data issue: false hasContentIssue false
  • English
  • Français

Streamwise dispersion and mixing in quasi-two-dimensional steady turbulent jets

Published online by Cambridge University Press:  12 September 2012

Julien R. Landel ,
C. P. Caulfield  and
Andrew W. Woods
Julien R. Landel*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Andrew W. Woods
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: jl501@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate experimentally and theoretically the streamwise transport and dispersion properties of steady quasi-two-dimensional plane turbulent jets discharged vertically from a slot of width 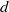into a fluid confined between two relatively close rigid boundaries with gap 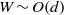. We model the evolution in time and space of the concentration of passive tracers released in these jets using a one-dimensional time-dependent effective advection–diffusion equation. We make a mixing length hypothesis to model the streamwise turbulent eddy diffusivity such that it scales like 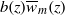, where is the streamwise coordinate, 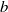is the jet width, 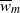is the maximum time-averaged vertical velocity. Under these assumptions, the effective advection–diffusion equation for 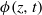, the horizontal integral of the ensemble-averaged concentration, is of the form 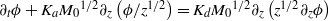, where is time, 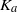(the advection parameter) and 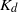(the dispersion parameter) are empirical dimensionless parameters which quantify the importance of advection and dispersion, respectively, and 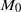is the source momentum flux. We find analytical solutions to this equation for 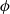in the cases of a constant-flux release and an instantaneous finite-volume release. We also give an integral formulation for the more general case of a time-dependent release, which we solve analytically when tracers are released at a constant flux over a finite period of time. From our experimental results, whose concentration distributions agree with the model, we find that 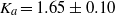and 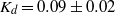, for both finite-volume releases and constant-flux releases using either dye or virtual passive tracers. The experiments also show that streamwise dispersion increases in time as 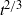. As a result, in the case of finite-volume releases more than 50 % of the total volume of tracers is transported ahead of the purely advective front (i.e. the front location of the tracer distribution if all dispersion mechanisms are ignored and considering a ‘top-hat’ mean velocity profile in the jet); and in the case of constant-flux releases, at each instant in time, approximately 10 % of the total volume of tracers is transported ahead of the advective front.

JFM classification

Wakes/Jets: Jets Geophysical and Geological Flows: Shallow water flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 212 - 258
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Cenedese, C. & Dalziel, S. B. 1998 Concentration and depth fields determined by the light transmitted through a dyed solution. In Proceedings of the 8th International Symposium on Flow Visualization (ed. G. M. Carlomagno & I. Grant) ISBN 0 9533991 0 9, paper 061.Google Scholar
2. Chatwin, P. C. & Allen, C. M. 1985 Mathematical models of dispersion in rivers and estuaries. Annu. Rev. Fluid Mech. 17, 119–149.CrossRefGoogle Scholar
3. Chen, D. & Jirka, G. H. 1998 Linear stability analysis of turbulent mixing layers and jets in shallow water layers. J. Hydraul. Res. 36, 815–830.Google Scholar
4. Chen, D. & Jirka, G. H. 1999 LIF study of plane jet bounded in shallow water layer. J. Hydraul. Engng 125, 817–826.CrossRefGoogle Scholar
5. Coomaraswamy, I. A. 2011 Natural ventilation of buildings: time-dependent phenomena. PhD thesis, University of Cambridge.Google Scholar
6. Dalziel, S. B. 1992 Decay of rotating turbulence: some particle tracking experiments. Appl. Sci. Res. 49, 217–244.CrossRefGoogle Scholar
7. Dalziel, S. B., Patterson, M. D., Caulfield, C. P. & Coomaraswamy, I. A. 2008 Mixing efficiency in high-aspect-ratio Rayleigh–Taylor experiments. Phys. Fluids 20, 065106.CrossRefGoogle Scholar
8. Dracos, T., Giger, M. & Jirka, G. H. 1992 Plane turbulent jets in a bounded fluid layer. J. Fluid Mech. 241, 587–614.CrossRefGoogle Scholar
9. Dutkiewicz, S., Griffa, A. & Olson, D. B. 1993 Particle diffusion in a meandering jet. J. Geophys. Res., Oceans 98, 16,487–16,500.CrossRefGoogle Scholar
10. Fischer, H. B. 1973 Longitudinal dispersion and turbulent mixing in open-channel flow. Annu. Rev. Fluid Mech. 5, 59–78.CrossRefGoogle Scholar
11. Giger, M., Dracos, T. & Jirka, G. H. 1991 Entrainment and mixing in plane turbulent jets in shallow water. J. Hydraul. Res. 29, 615–642.CrossRefGoogle Scholar
12. Gradshteyn, I. S. & Ryzhik, I. M. 2007 Table of Integrals, Series, and Products, seventh edition. Elsevier.Google Scholar
13. Jirka, G. H. 2001 Large scale flow structures and mixing processes in shallow flows. J. Hydraul. Res. 39, 567–573.CrossRefGoogle Scholar
14. Jirka, G. H. & Uijttewaal, W. S. J. 2004 Shallow flows: a definition. In Shallow Flows (ed. Jirka, G. H. & Uijttewaal, W. S. J. ). pp. 3–11. Taylor & Francis.CrossRefGoogle Scholar
15. Landel, J. R., Caulfield, C. P. & Woods, A. W. 2012 Meandering due to large eddies and the statistically self-similar dynamics of quasi-two-dimensional jets. J. Fluid Mech. 692, 347–368.CrossRefGoogle Scholar
16. Law, A. W. K. 2006 Velocity and concentration distributions of round and plane turbulent jets. J. Engng Math. 56, 69–78.CrossRefGoogle Scholar
17. Lewis, R. 1997 Dispersion in Estuaries and Coastal Waters. Wiley.Google Scholar
18. Luo, K., Klein, M., Fan, J.-R. & Cen, K.-F. 2006 Effects on particle dispersion by turbulent transition in a jet. Phys. Lett. A 357, 345–350.CrossRefGoogle Scholar
19. MacCready, P. & Geyer, W. R. 2010 Advances in estuarine physics. Annu. Rev. Mar. Sci. 2, 35–58.CrossRefGoogle ScholarPubMed
20. Mathieu, J. & Scott, J. 2000 An Introduction to Turbulent Flow. Cambridge University Press.CrossRefGoogle Scholar
21. Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
22. National Institute of Standards and Technology (2012) NIST Digital Library of Mathematical Functions, version 2012-03-23. http://dlmf.nist.gov/.Google Scholar
23. Paranthoën, P., Fouari, A., Dupont, A. & Lecordier, J. C. 1988 Dispersion measurements in turbulent flows (boundary layer and plane jet). Intl J. Heat Mass Transfer 31, 153–165.CrossRefGoogle Scholar
24. Picano, F., Sardina, G., Gualtieri, P. & Casciola, C. M. 2010 Anomalous memory effects on transport of inertial particles in turbulent jets. Phys. Fluids 22, 051705.CrossRefGoogle Scholar
25. Prandtl, L. 1925 A report on testing for built-up turbulence. Z. Angew. Math. Mech. 5, 136–139.CrossRefGoogle Scholar
26. Rowland, J. C., Stacey, M. T. & Dietrich, W. E. 2009 Turbulent characteristics of a shallow wall-bounded plane jet: experimental implications for river mouth hydrodynamics. J. Fluid Mech. 627, 423–449.CrossRefGoogle Scholar
27. Schefer, R. W., Kerstein, A. R., Namazian, M. & Kelly, J. 1994 Role of large-scale structure in a nonreacting turbulent CH4 jet. Phys. Fluids 6, 652–661.CrossRefGoogle Scholar
28. Sveen, J. K. & Dalziel, S. B. 2005 A dynamic masking technique for combined measurements of PIV and synthetic schlieren applied to internal gravity waves. Meas. Sci. Technol. 16, 1954–1960.CrossRefGoogle Scholar
29. Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
30. Taylor, G. I. 1954 The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. Lond. A 223, 446–468.Google Scholar
31. Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.CrossRefGoogle Scholar
32. Uberoi, M. S. & Singh, P. I. 1975 Turbulent mixing in a two-dimensional jet. Phys. Fluids 18, 764–769.CrossRefGoogle Scholar
33. Ward, P. R. B. & Fischer, H. B. 1971 Some limitations on use of one-dimensional dispersion equation, with comments. Water Res. Res. 7, 215.CrossRefGoogle Scholar
34. Yang, Y., Crowe, C. T., Chung, J. N. & Troutt, T. R. 2000 Experiments on particle dispersion in a plane wake. Intl J. Multiphase Flow 26, 1583–1607.CrossRefGoogle Scholar
35. Yannopoulos, P. & Noutsopoulos, G. 1990 The plane vertical turbulent buoyant jet. J. Hydraul. Res. 28, 565–580.CrossRefGoogle Scholar