Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ye, Huilin
Huang, Haibo
Sui, Yi
and
Lu, Xi-Yun
2016.
Dynamics of a nonspherical capsule in general flow.
Computers & Fluids,
Vol. 134-135,
Issue. ,
p.
31.
de Loubens, C.
Deschamps, J.
Edwards-Levy, F.
and
Leonetti, M.
2016.
Tank-treading of microcapsules in shear flow.
Journal of Fluid Mechanics,
Vol. 789,
Issue. ,
p.
750.
Dahl, Joanna B.
Narsimhan, Vivek
Gouveia, Bernardo
Kumar, Sanjay
Shaqfeh, Eric S. G.
and
Muller, Susan J.
2016.
Experimental observation of the asymmetric instability of intermediate-reduced-volume vesicles in extensional flow.
Soft Matter,
Vol. 12,
Issue. 16,
p.
3787.
Gounley, J.
Boedec, G.
Jaeger, M.
and
Leonetti, M.
2016.
Influence of surface viscosity on droplets in shear flow.
Journal of Fluid Mechanics,
Vol. 791,
Issue. ,
p.
464.
Gires, Pierre-Yves
Barthès-Biesel, Dominique
Leclerc, Eric
and
Salsac, Anne-Virginie
2016.
Transient behavior and relaxation of microcapsules with a cross-linked human serum albumin membrane.
Journal of the Mechanical Behavior of Biomedical Materials,
Vol. 58,
Issue. ,
p.
2.
Haward, S. J.
2016.
Microfluidic extensional rheometry using stagnation point flow.
Biomicrofluidics,
Vol. 10,
Issue. 4,
Gubspun, Jonathan
Gires, Pierre-Yves
Loubens, Clément de
Barthès-Biesel, Dominique
Deschamps, Julien
Georgelin, Marc
Leonetti, Marc
Leclerc, Eric
Edwards-Lévy, Florence
and
Salsac, Anne-Virginie
2016.
Characterization of the mechanical properties of cross-linked serum albumin microcapsules: effect of size and protein concentration.
Colloid and Polymer Science,
Vol. 294,
Issue. 8,
p.
1381.
Burshtein, Noa
Zografos, Konstantinos
Shen, Amy Q.
Poole, Robert J.
and
Haward, Simon J.
2017.
Inertioelastic Flow Instability at a Stagnation Point.
Physical Review X,
Vol. 7,
Issue. 4,
Xie, Kaili
de Loubens, Clément
Dubreuil, Frédéric
Gunes, Deniz Z.
Jaeger, Marc
and
Léonetti, Marc
2017.
Interfacial rheological properties of self-assembling biopolymer microcapsules.
Soft Matter,
Vol. 13,
Issue. 36,
p.
6208.
Gubspun, J
Loubens, C de
Trozzo, R
Deschamps, J
Georgelin, M
Edwards-Levy, F
and
Leonetti, M
2017.
Perturbations of the flow induced by a microcapsule in a capillary tube.
Fluid Dynamics Research,
Vol. 49,
Issue. 3,
p.
035501.
Koolivand, A.
and
Dimitrakopoulos, P.
2017.
Deformation of an elastic capsule in a microfluidic T-junction: settling shape and moduli determination.
Microfluidics and Nanofluidics,
Vol. 21,
Issue. 5,
Dimitrakopoulos, P.
2017.
Dumbbell formation for elastic capsules in nonlinear extensional Stokes flows.
Physical Review Fluids,
Vol. 2,
Issue. 6,
Plouraboué, Franck
Thiam, E. Ibrahima
Delmotte, Blaise
and
Climent, Eric
2017.
Identification of internal properties of fibres and micro-swimmers.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 473,
Issue. 2197,
p.
20160517.
Boedec, Gwenn
Leonetti, Marc
and
Jaeger, Marc
2017.
Isogeometric FEM-BEM simulations of drop, capsule and vesicle dynamics in Stokes flow.
Journal of Computational Physics,
Vol. 342,
Issue. ,
p.
117.
Liu, Yunqiao
He, Dongdong
Gong, Xiaobo
and
Huang, Huaxiong
2018.
Deformation of an encapsulated bubble in steady and oscillatory electric fields.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
567.
Das, Sudip
and
Thaokar, Rochish M.
2018.
Large deformation electrohydrodynamics of a Skalak elastic capsule in AC electric field.
Soft Matter,
Vol. 14,
Issue. 9,
p.
1719.
Das, Sudip
and
Thaokar, Rochish M.
2018.
Large-deformation electrohydrodynamics of an elastic capsule in a DC electric field.
Journal of Fluid Mechanics,
Vol. 841,
Issue. ,
p.
489.
Akbaridoust, Farzan
Philip, Jimmy
Hill, David R. A.
and
Marusic, Ivan
2018.
Simultaneous micro-PIV measurements and real-time control trapping in a cross-slot channel.
Experiments in Fluids,
Vol. 59,
Issue. 12,
Haward, S. J.
Hopkins, C. C.
Toda-Peters, K.
and
Shen, A. Q.
2019.
Microfluidic analog of an opposed-jets device.
Applied Physics Letters,
Vol. 114,
Issue. 22,
Degonville, Maximilien
Boedec, Gwenn
and
Leonetti, Marc
2019.
Oblate to prolate transition of a vesicle in shear flow.
The European Physical Journal E,
Vol. 42,
Issue. 9,
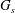 $G_{s}$. We conclude that the membrane of human serum albumin capsules obeys the generalized Hooke law with a Poisson ratio of 0.4. The shear elastic modulus is then determined by the combination of numerical and experimental variations of the Taylor parameter with the capillary number.
$G_{s}$. We conclude that the membrane of human serum albumin capsules obeys the generalized Hooke law with a Poisson ratio of 0.4. The shear elastic modulus is then determined by the combination of numerical and experimental variations of the Taylor parameter with the capillary number.