Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Michel, G.
and
Chini, G. P.
2019.
Multiple scales analysis of slow–fast quasi-linear systems.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 475,
Issue. 2223,
p.
20180630.
Nama, Nitesh
2019.
Mixing hot and cold with sound.
Journal of Fluid Mechanics,
Vol. 866,
Issue. ,
p.
1.
Das, Pradipta Kr.
Snider, Arthur David
and
Bhethanabotla, Venkat R.
2020.
Acoustic streaming in second-order fluids.
Physics of Fluids,
Vol. 32,
Issue. 12,
Burns, Keaton J.
Vasil, Geoffrey M.
Oishi, Jeffrey S.
Lecoanet, Daniel
and
Brown, Benjamin P.
2020.
Dedalus: A flexible framework for numerical simulations with spectral methods.
Physical Review Research,
Vol. 2,
Issue. 2,
Qiu, Wei
Joergensen, Jonas Helboe
Corato, Enrico
Bruus, Henrik
and
Augustsson, Per
2021.
Fast Microscale Acoustic Streaming Driven by a Temperature-Gradient-Induced Nondissipative Acoustic Body Force.
Physical Review Letters,
Vol. 127,
Issue. 6,
Daru, Virginie
Weisman, Catherine
Baltean-Carlès, Diana
and
Bailliet, Hélène
2021.
A numerical study of the coupling between Rayleigh streaming and heat transfer at high acoustic level.
The Journal of the Acoustical Society of America,
Vol. 150,
Issue. 6,
p.
4501.
O'Connor, Liam
Lecoanet, Daniel
and
Anders, Evan H.
2021.
Marginally stable thermal equilibria of Rayleigh-Bénard convection.
Physical Review Fluids,
Vol. 6,
Issue. 9,
Michel, Guillaume
and
Gissinger, Christophe
2021.
Cooling by Baroclinic Acoustic Streaming.
Physical Review Applied,
Vol. 16,
Issue. 5,
Kumar, Varun
Azharudeen, Mohammed
Pothuri, Charish
and
Subramani, Karthick
2021.
Heat transfer mechanism driven by acoustic body force under acoustic fields.
Physical Review Fluids,
Vol. 6,
Issue. 7,
Daru, Virginie
Weisman, Catherine
Baltean-Carlès, Diana
and
Bailliet, Hélène
2021.
Acoustically induced thermal effects on Rayleigh streaming.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
van Overveld, T. J. J. M.
Breugem, W.-P.
Clercx, H. J. H.
and
Duran-Matute, M.
2022.
Effect of the Stokes boundary layer on the dynamics of particle pairs in an oscillatory flow.
Physics of Fluids,
Vol. 34,
Issue. 11,
Baran, Błażej
Machaj, Krystian
Malecha, Ziemowit
and
Tomczuk, Krzysztof
2022.
Numerical Study of Baroclinic Acoustic Streaming Phenomenon for Various Flow Parameters.
Energies,
Vol. 15,
Issue. 3,
p.
854.
Rajendran, Varun Kumar
Solomon, Jefin
and
Subramani, Karthick
2022.
Heat transfer and flow patterns in a minichannel with various acoustic standing wave configurations and thermal boundary conditions.
International Journal of Heat and Mass Transfer,
Vol. 194,
Issue. ,
p.
122923.
Joergensen, Jonas Helboe
and
Bruus, Henrik
2023.
Theory and modeling of nonperturbative effects in thermoviscous acoustofluidics.
Physical Review E,
Vol. 107,
Issue. 1,
Malecha, Ziemowit
2023.
Three-dimensional numerical study of acoustic streaming phenomenon in rectangular resonator.
Fluid Dynamics Research,
Vol. 55,
Issue. 1,
p.
015504.
Gubaidullin, Amir A.
and
Pyatkova, Anna V.
2023.
The Effects of Heat Transfer through the Ends of a Cylindrical Cavity on Acoustic Streaming and Gas Temperature.
Mathematics,
Vol. 11,
Issue. 8,
p.
1840.
Zhong, Geyu
Liu, Yingwen
Guo, Xiaofeng
Royon, Laurent
and
Brunet, Philippe
2023.
Vibration-induced streaming flow near a sharp edge: Flow structure and instabilities in a large span of forcing amplitude.
Physical Review E,
Vol. 107,
Issue. 2,
Das, Pradipta Kr.
and
Bhethanabotla, Venkat R.
2023.
Development of a thermo-pressure acoustic model and its application in modeling three-dimensional acoustofluidic systems.
Physics of Fluids,
Vol. 35,
Issue. 3,
Massih, Jacques Abdul
Mushthaq, Remil
Michel, Guillaume
and
Chini, Gregory P.
2024.
Aspect-ratio-dependent heat transport by baroclinic acoustic streaming.
Journal of Fluid Mechanics,
Vol. 997,
Issue. ,
Rohan, Eduard
and
Moravcová, Fanny
2025.
Homogenization of the acoustic streaming in periodic rigid porous structures.
Journal of Sound and Vibration,
Vol. 618,
Issue. ,
p.
119252.
 $\unicode[STIX]{x1D716}$ and the streaming flow it drives in a thin channel with walls maintained at differing temperatures. Unlike classical Rayleigh streaming, the resulting mean flow arises at
$\unicode[STIX]{x1D716}$ and the streaming flow it drives in a thin channel with walls maintained at differing temperatures. Unlike classical Rayleigh streaming, the resulting mean flow arises at 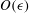 $O(\unicode[STIX]{x1D716})$ rather than at
$O(\unicode[STIX]{x1D716})$ rather than at 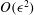 $O(\unicode[STIX]{x1D716}^{2})$. Consequently, fully two-way coupling between the waves and the mean flow is possible: the streaming is sufficiently strong to induce
$O(\unicode[STIX]{x1D716}^{2})$. Consequently, fully two-way coupling between the waves and the mean flow is possible: the streaming is sufficiently strong to induce 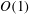 $O(1)$ rearrangements of the imposed background temperature and density fields, which modifies the spatial structure and frequency of the acoustic mode on the streaming time scale. A novel Wentzel–Kramers–Brillouin–Jeffreys analysis is developed to average over the fast wave dynamics, enabling the coupled system to be integrated strictly on the slow time scale of the streaming flow. Analytical solutions of the reduced system are derived for weak wave forcing and are shown to reproduce results from prior direct numerical simulations (DNS) of the compressible Navier–Stokes and heat equations with remarkable accuracy. Moreover, numerical simulations of the reduced system are performed in the regime of strong wave/mean-flow coupling for a fraction of the computational cost of the corresponding DNS. These simulations shed light on the potential for baroclinic acoustic streaming to be used as an effective means to enhance heat transfer.
$O(1)$ rearrangements of the imposed background temperature and density fields, which modifies the spatial structure and frequency of the acoustic mode on the streaming time scale. A novel Wentzel–Kramers–Brillouin–Jeffreys analysis is developed to average over the fast wave dynamics, enabling the coupled system to be integrated strictly on the slow time scale of the streaming flow. Analytical solutions of the reduced system are derived for weak wave forcing and are shown to reproduce results from prior direct numerical simulations (DNS) of the compressible Navier–Stokes and heat equations with remarkable accuracy. Moreover, numerical simulations of the reduced system are performed in the regime of strong wave/mean-flow coupling for a fraction of the computational cost of the corresponding DNS. These simulations shed light on the potential for baroclinic acoustic streaming to be used as an effective means to enhance heat transfer.

